Giải đề thi học kì 1 lý lớp 10 năm 2019 - 2020 Sở giáo dục Vĩnh Phúc

A. PHẦN TRẮC NGHIỆM (3 điểm)

Câu 1 : Đại lượng đặc trưng cho mức quán tính của một vật là

A. lực.                              B. trọng lượng.

C. vận tốc.                        D. khối lượng.

Câu 2 : Khối lượng Trái Đất, bán kính Trái Đất và hằng số hấp dẫn lần lượt là \(M,R,G\). Biểu thức của gia tốc rơi tự do ở gần mặt đất là

A.\(g = \dfrac{F}{{{R^2}}}\)

B. \(g = \dfrac{{GM}}{{{R^2}}}\)

C.\(g = \dfrac{{GM}}{R}\)

D. \(g = \dfrac{M}{{{R^2}}}\)

Câu 3 : Một quả cam khối lượng m đặt tại nơi có gia tốc trọng trường g. Khối lượng Trái Đất là M. Kết luận nào sau đây là đúng?

A. Trái Đất hút quả cam một lực bằng (M+m)g;

B. Quả cam hút Trái Đất một lực có độ lớn bằng mg.

C. Trái Đất hút quả cam một lực bằng Mg.

D. Quả cam hút Trái Đất một lực có độ lớn bằng Mg.

Câu 4 : Véc tơ gia tốc của vật chuyển động tròn đều

A. hướng vào tâm quỹ đạo.

B. Cùng hướng với véc tơ vận tốc.

C. ngược hướng với véc tơ vận tốc.x

D. Hướng ra xa tâm quỹ dao.

Câu 5 : Phép đo quãng đường đi S của vật rơi tự do có sai số tuyệt đối \(\Delta S = 0,1cm\) và giá trị trung bình là \(\overline S  = 10,0cm\). Sai số tỉ đối \(\delta S\) là tỉ số giữa sai số tuyệt đối và giá trị trung bình của đại lượng đo, tính bằng phần trăm. Giá trị của \(\delta S\) bằng

A.\(1\% \)                          B. \(5\% \)                         C. \(11\% \)                       D. \(10\% \)

Câu 6 : Đơn vị của hệ số đàn hồi của lò xo là

A. \(N/s\)                          B. \(N/{m^2}\)                 

C. \(N/m\)                         D. \(m/N\)

Câu 7 : Một vật chuyển động thẳng nhanh dần đều có gia tốc \(2m/{s^2}\), thời gian tăng vận tốc từ \(10m/s\) đến \(40m/s\) bằng

A. \(20s\)             B. \(25s\)             C. \(10s\)             D. \(15s\)

Câu 8 : Cặp “lực và phản lực” trong định luật III Niuton

A. không bằng nhau về độ lớn.

B. tác dụng vào hai vật khác nhau

C. bằng nhau về độ lớn nhưng không cùng giá.

D. tác dụng vào cùng một vật.

Câu 9 : Chuyển động của một vật rơi tự do là

A. chuyển động tròn đều.

B. chuyển động thẳng chậm dần đều

C. chuyển động thẳng đều.

D. chuyển động thẳng nhanh dần đều.

Câu 10 : Có hai lực đồng qui có độ lớn bằng \(9N\) và \(12N\). Trong số các giá trị sau đây, giá trị nào có thể là độ lớn của hợp lực?

A. \(1N\)                B. \(25N\)             C. \(2N\)                 D. \(15N\)

Câu 11. Một vật chuyển động thẳng có phương trình \(x = {x_0} + {v_0}t + \dfrac{1}{2}a{t^2}\), trong đó đại lượng \(a\) là

A. vận tốc lúc đầu.                          B. gia tốc.

C. quãng đường đi được.                 D. tọa độ lúc đầu.

Câu 12. Một vật chuyển động thẳng đều có tốc độ \(v\), quãng đường vật đi được trong thời gian t là

A.\(s = vt\)                              B. \(s = v + t\)

C. \(s = v{t^2}\)                     D. \(s = {v^2}t\)

B. PHẦN TỰ LUẬN (7,0 điểm)

Câu 13: (3 điểm:)

a) Sự rơi tự do là gì? Viết công thức vận tốc và quãng đường đi của vật rơi tự do.

b) Viết hệ thức của lực hấp dẫn giữa hai chất điểm và giải thích các đại lượng có trong hệ thức này.

c) Nêu những đặc điểm về điểm đặt, phương, chiều, độ lớn của lực đàn hồi lò xo.

Câu 14: (1 điểm) Cho phương trình chuyển động thẳng đều \(x = 10 + 5t\) ( \(x\) tính bằng m; t tính bằng s). Hãy xác định tọa độ ban đầu, vận tốc, chiều chuyển động và tọa độ của vật sau 10s.

Câu 15: (1 điểm) Một chiếc thuyền chuyển động thẳng đều cùng chiều dòng nước, sau một giờ đi được 12km đối với bờ. Một khúc gỗ trôi theo dòng nước với vận tốc 2km/h đối với bờ. Hãy tính vận tốc của thuyền so với nước.

Câu 16: (1 điểm) Một vật có khối lượng \(500g\) đang chuyển động thẳng đều với vận tốc \(18km/h\) thì chịu tác dụng của một lực \(\overrightarrow F \) có độ lớn \(2N\) ngược chiều chuyển động của vật.

a) Tính độ lớn gia tốc của vật khi chịu tác dụng của lực \(\overrightarrow F \).

b) Tính quãng đường và thời gian vật chuyển động từ khi chịu tác dụng của lực \(\overrightarrow F \) cho đến khi dừng lại.

Câu 17: (1 điểm) Một lò xo treo thẳng đứng, đầu trên cố định. Khi treo vào đầu dưới lò xo vật khối lượng \({m_1} = 500g\) thì chiều dài lò xo bằng \(25cm\), còn khi treo vật \({m_2} = 800g\) thì chiều dài bằng \(28cm\). Lấy \(g = 10m/{s^2}\).

a) Tìm chiều dài tự nhiên và độ cứng của lò xo.

b) Vẽ đồ thị lực đàn hồi của lò xo theo chiều dài lò xo thay đổi từ 12cm, đến 28cm.

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

I.  TRẮC NGHIỆM

 Câu 1 (NB):

Phương pháp:

Sử dụng lí thuyết về quán tính

Cách giải:

Đại lượng đặc trưng cho mức quán tính của một vật là khối lượng.

Chọn D

Câu 2 (TH):

Phương pháp:

Sử dụng biểu thức xác định gia tốc rơi tự do ở mặt đất

Cách giải:

Biểu thức của gia tốc rơi tự do ở gần mặt đất: \(g = \dfrac{{GM}}{{{R^2}}}\)

Chọn B

Câu 3 (TH):

Phương pháp:

Vận dụng biểu thức lực hấp dẫn

Cách giải:

Lực hấp dẫn giữa quả cam và Trái Đất: \(F = G\dfrac{{Mm}}{{{R^2}}} = mg\)

Chọn B

Câu 4 (TH):

Phương pháp:

Sử dụng lí thuyết về lực hướng tâm và gia tốc hướng tâm

Cách giải:

Véc-tơ gia tốc của vật chuyển động tròn đều luôn hướng vào tâm quỹ đạo.

Chọn A

Câu 5 (TH):

Phương pháp:

Sử dụng biểu thức tính sai số tỉ đối: \(\delta S = \dfrac{{\Delta S}}{{\overline S }}.100\% \)

Cách giải:

Sai số tỉ đối: \(\delta S = \dfrac{{\Delta S}}{{\overline S }}.100\%  = \dfrac{{0,1}}{{10,0}}.100\%  = 1\% \)

Chọn A

Câu 6 (NB):

Phương pháp:

Sử dụng lí thuyết về các lượng và đơn vị của các đại lượng của lực đàn hồi

Cách giải:

Hệ số đàn hồi của lò xo: \(k\)  có đơn vị \(N/m\)

Chọn C

Câu 7 (VD):

Phương pháp:

Áp dụng biểu thức: \(a = \dfrac{{\Delta v}}{{\Delta t}}\)

Cách giải:

Ta có:

Gia tốc: \(a = \dfrac{{\Delta v}}{{\Delta t}}\)

\( \Rightarrow \) Thời gian tăng vận tốc: \(\Delta t = \dfrac{{\Delta v}}{a} = \dfrac{{40 - 10}}{2} = 15s\)

Chọn D

Câu 8 (TH):

Phương pháp:

Sử dụng lí thuyết về lực và phản lực của định luật III - Niuton

Cách giải:

Cặp lực và phản lực trong định luật III – Niuton cùng phương, ngược chiều, cùng độ lớn và được đặt vào 2 vật khác nhau.

Chọn B

Câu 9 (TH):

Phương pháp:

Sử dụng lí thuyết về chuyển động rơi tự do

Cách giải:

Ta có:

Chuyển động của một vật rơi tự do là chuyển động thẳng nhanh dần đều.

Chọn D

Câu 10 (TH):

Phương pháp:

Vận dụng điều kiện của hợp lực: \(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\)

Cách giải:

Ta có:

Hợp lực: \(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\)

\( \Leftrightarrow 3N \le F \le 21N\)

Từ các phương án \( \Rightarrow F = 15N\) thỏa mãn

Chọn D

Câu 11 (TH):

Phương pháp:

Sử dụng lí thuyết về chuyển động thẳng biến đổi đều

Cách giải:

\(x = {x_0} + {v_0}t + \dfrac{1}{2}a{t^2}\)

Trong đó: \(a\) - gia tốc của chuyển động

Chọn B

Câu 12 (TH):

Phương pháp:

Sử dụng biểu thức tính quãng đường của chuyển động thẳng đều.

Cách giải:

Quãng đường đi được của vật chuyển động thẳng đều: \(s = vt\)

Chọn A

B. PHẦN TỰ LUẬN

Câu 13 (NB)

Phương pháp:

a) Sử dụng lý thuyết về sự rơi tự do SGK VL 10 trang 25

b) Sử dụng biểu thức của lực hấp dẫn SGK VL 10 trang 68

c) Sử dụng lí thuyết về lực đàn hồi của lò xo SGK VL 10 trang 71

Cách giải:

a)

- Sự rơi tự do là sự rơi chỉ dưới tác dụng của trọng lực.

- Các công thức:

+ Vận tốc: \(v = gt\)

+ Quãng đường đi: \(s = \dfrac{1}{2}g{t^2}\)

b) Hệ thức của lực hấp dẫn: \({F_{hd}} = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}\)

Trong đó:

- \({m_1},{m_2}\): là khối lượng của hai chất điểm

- \(r\): là khoảng cách giữa chúng

- \(G = 6,{67.10^{ - 11}}N.{m^2}/k{g^2}\): hằng số hấp dẫn.

c) Đặc điểm của lực đàn hồi lò xo:

- Điểm đặt: Đặt tại 2 đầu của lò xo

- Phương: trùng với phương của trục lò xo

- Chiều: ngược với chiều biến dạng của lò xo

- Độ lớn: \({F_{dh}} = k\left| {\Delta l} \right|\)

Câu 14 (VD)

Phương pháp:

Vận dụng biểu thức chuyển động thẳng đều: \(x = {x_0} + vt\)

Cách giải:

Ta có phương trình chuyển động: \(x = 10 + 5t\)

- Tọa độ ban đầu của vật: \({x_0} = 10m\)

- Vận tốc của vật: \(v = 5m/s\)

- Nhận thấy \(v > 0 \Rightarrow \) vật chuyển động theo chiều dương.

- Tọa độ của vật sau 10s: \(x = 10 + 5.10 = 60m\)

Câu 15 (VD)

Phương pháp:

Sử dụng công thức cộng vận tốc: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Cách giải:

(1) Thuyền

(2) Nước

(3) Bờ

+ Vận tốc của thuyền so với bờ: \(\overrightarrow {{v_{13}}} \)

+ Vận tốc của thuyền so với nước: \(\overrightarrow {{v_{12}}} \)

+ Vận tốc của nước so với bờ: \(\overrightarrow {{v_{23}}} \)

Ta có:

\({v_{13}} = \dfrac{{12}}{1} = 12km/h\)

\({v_{23}} = 2km/h\)

Theo công thức cộng vận tốc, ta có: \(\overrightarrow {{v_{13}}}  = \overrightarrow {{v_{12}}}  + \overrightarrow {{v_{23}}} \)

Lại có: \(\overrightarrow {{v_{12}}}  \uparrow  \uparrow \overrightarrow {{v_{23}}}  \Rightarrow {v_{13}} = {v_{12}} + {v_{23}}\)

\( \Rightarrow {v_{12}} = {v_{13}} - {v_{23}} = 12 - 2 = 10km/h\)

Câu 16 (VD)

Phương pháp:

a) Sử dụng biểu thức định luật II – Niuton: \(F = ma\)

b)

+ Sử dụng hệ thức độc lập: \({v^2} - v_0^2 = 2as\)

+ Sử dụng biểu thức: \(a = \dfrac{{\Delta v}}{{\Delta t}}\)

Cách giải:

a) Gia tốc của vật: \(a = \dfrac{{ - F}}{m} = \dfrac{{ - 2}}{{0,5}} =  - 4m/{s^2}\)

b)

Vận tốc ban đầu của vật \({v_0} = 18km/h = 5m/s\)

+ Quãng đường vật đi được cho đến khi dừng lại: \(s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{0 - {5^2}}}{{2.\left( { - 4} \right)}} = 3,125m\)

+ Thời gian vật chuyển động cho đến khi dừng lại: \(t = \dfrac{{\Delta v}}{a} = \dfrac{{v - {v_0}}}{a} = \dfrac{{0 - 5}}{{ - 4}} = 1,25s\)

Câu 17 (VD)

Phương pháp:

a) Vận dụng biểu thức định luật Húc: \({F_{dh}} = k\left| {\Delta l} \right|\)

b) Vẽ đồ thị

Cách giải:

a)

Con lắc lò xo treo thẳng đứng, tại vị trí cân bằng lực đàn hồi cân bằng với trọng lực của vật.

+ Khi treo vật có khối lượng \({m_1} = 0,5kg\): \({F_{d{h_1}}} = k\left( {{l_1} - {l_0}} \right) = {P_1}\)  (1)

+ Khi treo vật có khối lượng \({m_2} = 0,8kg\): \({F_{dh2}} = k\left( {{l_2} - {l_0}} \right) = {P_2}\)  (2)

Lấy \(\dfrac{{\left( 1 \right)}}{{\left( 2 \right)}}\) ta được: \(\dfrac{{{F_{dh1}}}}{{{F_{d{h_2}}}}} = \dfrac{{{P_1}}}{{{P_2}}} \Leftrightarrow \dfrac{{k\left( {{l_1} - {l_0}} \right)}}{{k\left( {{l_2} - {l_0}} \right)}} = \dfrac{{{m_1}g}}{{{m_2}g}}\)

\(\begin{array}{l} \Rightarrow \dfrac{{{l_1} - {l_0}}}{{{l_2} - {l_0}}} = \dfrac{{{m_1}}}{{{m_2}}} = \dfrac{{0,5}}{{0,8}} = 0,625\\ \Leftrightarrow \dfrac{{25 - {l_0}}}{{28 - {l_0}}} = 0,625\\ \Rightarrow {l_0} = 20cm\end{array}\)

Thay ngược lại (1) suy ra độ cứng của lò xo: \(k = 100N/m\)

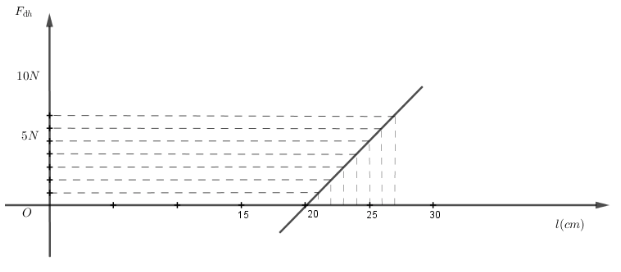
b)

Lập bảng giá trị của \({F_{dh}}\) theo chiều dài lò xo

\({F_{dh}} = k\left| {\Delta l} \right|\)