Đề kiểm tra 45 phút chương 2 phần Hình học 8 - Đề số 2

Đề bài

Hãy chọn câu trả lời đúng

Câu 1: Một hình thang có diện tích \(465{m^2}\), chiều cao \(15m\), hiệu hai đáy bằng \(8m.\) Đáy nhỏ của hình thang đó bằng

\(\begin{array}{l}(A)\,27m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,\,24m\\(C)\,\,14m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,\,35m\end{array}\)

Câu 2: Một hình thoi có chu vi \(52cm\), một đường chéo bằng \(24cm.\) Diện tích hình thoi đó bằng

\(\begin{array}{l}(A)\,\,100c{m^2}\,\,\\(B)\,\,120c{m^2}\\(C)\,\,240c{m^2}\\(D)\,\,1920c{m^2}\end{array}\)

Câu 3: Hình bình hành \(ABCD\) có \(\widehat D = {30^o},AD = a,AB = b.\)  Diện tích hình bình hành đó bằng

\(\begin{array}{l}(A)\,\,\dfrac{{ab}}{4}\\(B)\,\,\dfrac{{ab}}{{\sqrt 2 }}\\(C)\,\,\dfrac{{ab\sqrt 3 }}{4}\\(D)\,\,\dfrac{{ab}}{2}\end{array}\)

Câu 4:

a) Định nghĩa đa giác đều.

b) Tính số đo mỗi góc của bát giác đều (tức là đa giác đều \(8\) cạnh).

Câu 5:

Cho tam giác \(ABC\) vuông cân tại \(A\), \(AB = AC = 4cm.\)  Lấy điểm \(D\) thuộc tia đối của tia \(AB\), lấy điểm \(E\) thuộc tia đối của tia \(AC\) sao cho \(AD = AE = 2cm.\)

a) Tính diện tích tam giác \(ABC.\)

b) Tính diện tích tam giác \(DEC.\)

c) Tứ giác \(BCDE\) là hình gì? Vì sao?

d) Tính diện tích tứ giác \(BCDE.\)

Lời giải chi tiết

Câu 1:

Phương pháp:

Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.

$$S = {1 \over 2}\left( {a + b} \right).h$$

Lời giải:

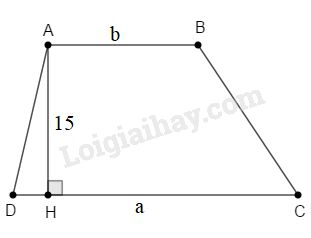
Gọi độ dài đáy lớn và đáy nhỏ của hình thang lần lượt là \(a, b\).

Ta có:

 \(\begin{array}{l}{S_{ABCD}} = \dfrac{1}{2}\left( {a + b} \right).15 = 465\,\,\left( {{m^2}} \right)\\ \Rightarrow a + b = \dfrac{{465.2}}{{15}}\\ \Rightarrow a + b = 62\,\,\,\,\,\,\,\,\,(1)\end{array}\)

Theo đề bài \(a - b = 8 \Rightarrow a = 8 + b\,\,\,\,\,\,(2)\)

Thay (2) vào (1) ta được:

\(\begin{array}{l}8 + b + b = 62\\ \Rightarrow 2b = 62 - 8\\ \Rightarrow 2b = 54\\ \Rightarrow b = 54:2 = 27\,\,\left( m \right)\\ \Rightarrow a = 8 + 27 = 35\,\left( m \right)\end{array}\)

Chọn A.

Câu 2:

Phương pháp:

- Định lí Pytago: Trong tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.

- Diện tích hình thoi có hai đường chéo \({d_1};\,\,{d_2}\)  là: \(\dfrac{1}{2}.{d_1}.{d_2}\)

Lời giải:

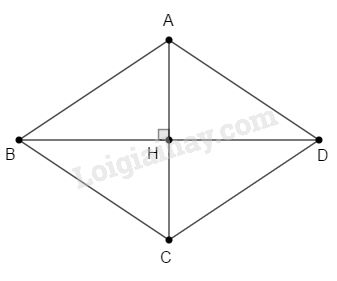
Giả sử hình thoi \(ABCD\) có chu vi là \(52cm\) và \(BD=24 cm\).

\(AB = 52:4 = 13\,\,\left( {cm} \right)\)

Gọi \(H\) là giao điểm hai đường chéo hình thoi.

\(BH = BD:2 = 24:2 = 12\,\,\left( {cm} \right)\)

Áp dụng định lí Pytago vào tam giác vuông \(ABH\) ta có:

\(\begin{array}{l}A{B^2} = B{H^2} + A{H^2}\\ \Rightarrow A{H^2} = A{B^2} - B{H^2} \\\;\;\;\;\;\;\;\;\;\;\;\;\;= {13^2} - {12^2} = 25\\ \Rightarrow AH = \sqrt {25}  = 5\,\,\left( {cm} \right)\\ \Rightarrow AC = 2AH = 2.5 = 10\,\left( {cm} \right)\\ \Rightarrow {S_{ABCD}} = \dfrac{1}{2}.BD.AC \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \dfrac{1}{2}.24.10 = 120\,\left( {c{m^2}} \right)\end{array}\)

Chọn B.

Câu 3:

Phương pháp:

- Trong tam giác vuông có một góc \({30^o}\)  cạnh đối diện với góc \({30^o}\) bằng nửa cạnh huyền.

- Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.

\(S = ah\) 

Lời giải:

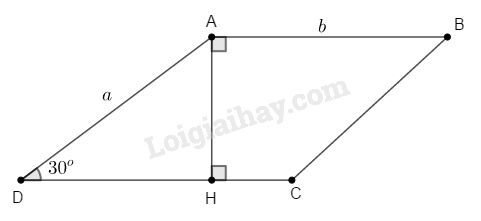
Dựng \(AH \bot DC\,\,\left( {H \in CD} \right)\)

Xét  tam giác \(AHD\) vuông tại \(H\) có \(\widehat {ADH} = {30^o}\)

\(\begin{array}{l} \Rightarrow AH = \dfrac{1}{2}AD = \dfrac{1}{2}a\\ \Rightarrow {S_{ABCD}} = AH.CD = \dfrac{1}{2}a.b = \dfrac{{ab}}{2}\end{array}\)

Chọn D.

Câu 4:

Phương pháp:

- Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

- Tổng các góc trong của hình n-giác bằng \(\left( {n - 2} \right){.180^o}\)

Lời giải:

a) Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

b) Số đo mỗi góc của bát giác đều là:

\(\dfrac{{\left( {8 - 2} \right){{.180}^o}}}{8} = {135^o}\)

Câu 5:

Phương pháp:

Sử dụng: 

- Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

$$S = {1 \over 2}ah$$

(\(S\) là diện tích, \(a\) là cạnh tam giác, \(h\) là chiều cao tương ứng với cạnh \(a\))

- Hình thang là tứ giác có hai cạnh đối song song.

- Hình thang có hai đường chéo bằng nhau là hình thang cân.

Lời giải:

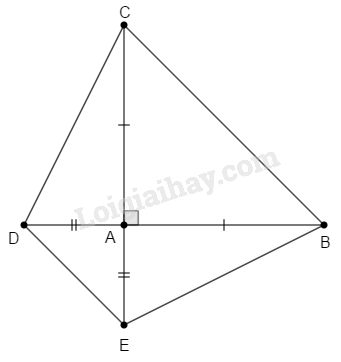
a) \({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.4.4 \)\(\,= 8\,\left( {c{m^2}} \right)\)

b)

 \(\begin{array}{l}{S_{DEC}} = \dfrac{1}{2}.AD.EC\\ \,\,\,\,\,\,\,\,\,\,\,\, \;\;= \dfrac{1}{2}.2.\left( {EA + AC} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, \;\;= \dfrac{1}{2}.2.\left( {2 + 4} \right) = 6\,\left( {c{m^2}} \right)\end{array}\)

c) \(\Delta AED\)  vuông cân tại \(A.\)

\( \Rightarrow \widehat {AED} = {45^o}\)

\(\Delta ABC\)  vuông cân tại \(A.\)

\( \Rightarrow \widehat {ACB} = {45^o}\)

Do đó

 \(\begin{array}{l}\widehat {AED} = \widehat {ACB} = {45^o}\\ \Rightarrow BC//DE\end{array}\)

(\(2\) góc so le trong bằng nhau)

Suy ra \(BCDE\) là hình thang.

Mặt khác:

\(\begin{array}{l}BD = AB + AD = 4 + 2 = 6\\CE = AC + AE = 4 + 2 = 6\\ \Rightarrow BD = CE\end{array}\)

Hình thang \(BCDE\) có hai đường chéo bằng nhau nên là hình thang cân.

d)

\(\begin{array}{l}{S_{EBC}} = \dfrac{1}{2}AB.CE \\\;\;\;\;\;\;\;\;\;= \dfrac{1}{2}.4.6 = 12\,\,\left( {c{m^2}} \right)\\{S_{BCDE}} = {S_{DEC}} + {S_{EBC}}\\\;\;\;\;\;\;\;\;\;\;\; = 6 + 12 = 18\,\,\left( {c{m^2}} \right)\end{array}\)