Đề kiểm tra 45 phút chương 2 phần Hình học 8 - Đề số 1

Đề bài

Hãy chọn câu trả lời đúng (trong các câu từ 1 đến 3).

Câu 1: Một tam giác có diện tích bằng diện tích hình vuông cạnh \(14m.\)

Một cạnh của tam giác đó bằng 16m. Chiều cao ứng với cạnh đó bằng

\(\begin{array}{l}(A)\,\,24,5\,m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,\,49\,\,m\\(C)\,\,32m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,12,25m\end{array}\)

Câu 2: Một hình thang cân có hai đường chéo vuông góc, mỗi đường chéo dài \(8cm.\) Diện tích hình thang cân đó bằng

\(\begin{array}{l}(A)\,\,16c{m^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,\,32c{m^2}\\(C)\,\,64c{m^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,\,\,48c{m^2}\end{array}\)

Câu 3: Hình bình hành \(ABCD\) có \(AD = 6cm,CD = 10cm,AC = 8cm.\)  Diện tích hình bình hành đó bằng

\(\begin{array}{l}(A)\,\,24c{m^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(B)\,\,42c{m^2}\\(C)\,\,48c{m^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(D)\,\,96c{m^2}\end{array}\)

Câu 4:

a) Tổng các góc trong của hình n-giác bằng bao nhiêu?

b) Tính tổng số đo các góc của đa giác có \(8\) cạnh.

c) Tính số cạnh của một đa giác có tổng các góc trong bằng \({1800^o}.\)

Câu 5: Hình thang \(ABCD\) có \(\widehat A = \widehat D = {90^o},AB = AD = 4cm,\)\(\,CD = 8cm.\)

a) Tính diện tích tam giác \(ABD.\)

b) Tính diện tích hình thang \(ABCD.\)

c) Tính số đo góc \(BCD.\)

Lời giải chi tiết

Câu 1:

Phương pháp:

Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

$$S = {1 \over 2}ah$$

(\(S\) là diện tích, \(a\) là cạnh tam giác, \(h\) là chiều cao tương ứng với cạnh \(a\)) 

Lời giải:

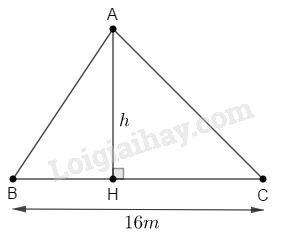
\({S_{ABC}} = 14.14 = 196\left( {{m^2}} \right)\)

Gọi \(h\) là độ dài chiều cao của tam giác \(ABC\) ứng với cạnh \(16m\).

Ta có

\(\begin{array}{l}{S_{ABC}} = \dfrac{1}{2}.16.h = 196\\ \Rightarrow h = \dfrac{{196.2}}{{16}} = 24,5\,\left( m \right)\end{array}\)

Chọn A.

Câu 2:

Phương pháp:

Diện tích của một tứ giác có hai đường chéo vuông góc bằng nửa tích độ dài hai đường chéo đó.

\({S_{ABCD}}=\dfrac{1}{2} AC. BD\)

Lời giải:

Gọi \({d_1};\,{d_2}\)  là độ dài hai đường chéo của hình thang cân đã cho.

Hình thang cân có hai đường chéo bằng nhau nên \({d_1} = {d_2} = 8\,\,cm\)

Hai đường chéo vuông góc nên diện tích hình thang cân là:

\(S = \dfrac{1}{2}{d_1}.{d_2} = \dfrac{1}{2}.8.8 = 32\,\left( {c{m^2}} \right)\)

Chọn B.

Câu 3:

Phương pháp:

- Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.

\(S = ah\) 

- Định lí Pytago đảo: Trong một tam giác nếu bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

Lời giải:

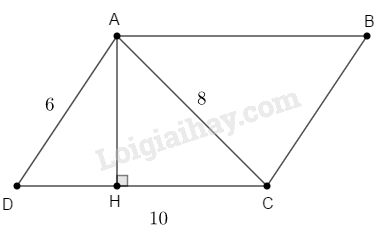
Xét \(\Delta ACD\)  có:

\(\begin{array}{l}A{D^2} + A{C^2} = {6^2} + {8^2} = 100\\C{D^2} = {10^2} = 100\\ \Rightarrow A{D^2} + A{C^2} = C{D^2}\end{array}\)

Theo định lí Pytago đảo \(\Delta ACD\) vuông tại \(A\).

Gọi \(AH\) là chiều cao của hình bình hành.

\(\begin{array}{l}{S_{ACD}} = \dfrac{1}{2}AD.AC = \dfrac{1}{2}AH.DC\\ \Rightarrow AD.AC = AH.DC\\{S_{ABCD}} = AH.DC = AD.AC\\\;\;\;\;\;\;\;\;\;\;\;\; = 6.8 = 48\,\,\left( {c{m^2}} \right)\end{array}\)

Chọn C.

Câu 4:

Phương pháp:

Tổng các góc trong của hình n-giác bằng \(\left( {n - 2} \right){.180^o}\)

Lời giải:

a) Tổng các góc trong của hình n-giác bằng \(\left( {n - 2} \right){.180^o}\)

b) Tổng số đo các góc của đa giác có \(8\) cạnh là:

\(\left( {8 - 2} \right){.180^o} = {6.180^o} = {1080^o}\)

c) Gọi \(n\,\,\left( {n \in N;\,n > 2} \right)\)  là số cạnh của đa giác cần tìm.

Ta có:

\(\begin{array}{l}\left( {n - 2} \right){.180^o} = {1800^o}\\ \Rightarrow n - 2 = {1800^o}:{180^o}\\ \Rightarrow n - 2 = 10\\ \Rightarrow n = 10 + 2 = 12\end{array}\)

Câu 5:

Phương pháp:

a) Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

$$S = {1 \over 2}ah$$

(\(S\) là diện tích, \(a\) là cạnh tam giác, \(h\) là chiều cao tương ứng với cạnh \(a\))

b) Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.

$$S = {1 \over 2}\left( {a + b} \right).h$$

c) Tam giác cân có hai góc đáy bằng nhau

Lời giải:

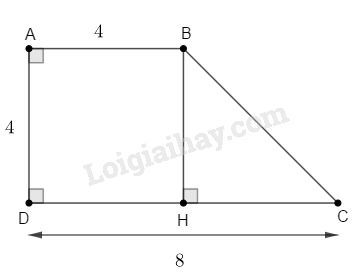
a) \({S_{ABD}} = \dfrac{1}{2}.AB.AD = \dfrac{1}{2}.4.4 \)\(\,= 8\,\,\left( {c{m^2}} \right)\)

\({S_{ABCD}} = \dfrac{1}{2}.\left( {AB + CD} \right).AD \)\(\,= \dfrac{1}{2}.\left( {4 + 8} \right).4 = 24\,\,\left( {c{m^2}} \right)\)

c) Kẻ \(BH \bot CD\) .

Tứ giác \(ABHD\) có \(\widehat {BAD} = \widehat {ADH} = \widehat {DHB} = {90^o}\)  nên là hình chữ nhật.

Mà \(AB = AD\)  nên \(ABHD\) là hình vuông.

\(\begin{array}{l} \Rightarrow DH = BH = 4cm\,;\,\\ \Rightarrow HC = DC - DH = 8 - 4 = 4cm\end{array}\)

Do đó \(\Delta BHC\)  vuông cân tại \(H.\)

\( \Rightarrow \widehat {HBC} = \widehat {HCB} = \dfrac{{{{90}^o}}}{2} = {45^o}\)

Hay \(\widehat {BCD} = {45^o}.\)