Giải câu 1, 2, 3, 4 trang 61, 62

Bài 1

Tính: 

a) \(\dfrac{7}{8} \times 1\dfrac{2}{7} =  \ldots \)

b) \(\dfrac{4}{5}:2\dfrac{1}{7} =  \ldots \)

c) \(5,18 \times 0,75 + 15,38 =  \ldots \)

d) 7 giờ 15 phút – 7 giờ 15 phút : 3 = ……..

e) Số trung bình cộng của 13; 36; 27 và 72 là ……..

Phương pháp giải:

- Đổi hỗn số thành phân số rồi thực hiện phép nhân hoặc phép chia hai phân số như thông thường.

- Biểu thức có phép cộng, phép trừ, phép nhân, phép chia thì ta thực hiện phép nhân, phép chia trước; thực hiện phép cộng, phép trừ sau.

- Muốn tìm trung bình cộng của nhiều số ta lấy tổng của các số đó chia cho số các số hạng.

Lời giải chi tiết:

a) \(\dfrac{7}{8} \times 1\dfrac{2}{7} = \dfrac{7}{8} \times \dfrac{9}{7} = \dfrac{{7 \times 9}}{{8 \times 7}} = \dfrac{9}{8}\)

b) \(\dfrac{4}{5}:2\dfrac{1}{7} = \dfrac{4}{5}:\dfrac{{15}}{7} = \dfrac{4}{5} \times \dfrac{7}{{15}} \)\(= \dfrac{{28}}{{75}}\)

c) \(5,18 \times 0,75 + 15,38\)

    \(= 3,885 + 15,38\)

    \(= 19,265\)  

d) 7 giờ 15 phút – 7 giờ 15 phút : 3

    = 7 giờ 15 phút – 2 giờ 25 phút

    = 6 giờ 75 phút – 2 giờ 25 phút

    = 4 giờ 50 phút

e) Số trung bình cộng của 13; 36; 27 và 72 là:

            (13 + 36 + 27 + 72) : 4 = 37

Bài 2

Một người đi xe máy đi 1,5 giờ đầu với vận tốc 38km/giờ, 2 giờ sau đi với vận tốc 35km/giờ. Hỏi người đi xe máy đó đi được quãng đường dài bao nhiêu ki-lô-mét? 

Phương pháp giải:

- Tìm quãng đường đi được trong 1,5 giờ đầu ta lấy vận tốc đi trong 1,5 giờ đầu nhân với thời gian.

- Tìm quãng đường đi được trong 2 giờ sau ta lấy vận tốc đi trong 2 giờ sau nhân với thời gian.

- Tìm quãng đường người đó đã đi được ta lấy quãng đường đi được trong 1,5 giờ đầu cộng với quãng đường đi được trong 2 giờ sau.

Lời giải chi tiết:

Trong \(1,5\) giờ đầu người đó đi quãng đường dài số ki-lô-mét là:

              \(38 × 1,5 = 57\;(km)\) 

Trong \(2\) giờ sau người đó đi quãng đường dài số ki-lô-mét là:

              \(35 × 2 = 70\;(km)\) 

Người đi xe máy đó đi được quãng đường dài số ki-lô-mét là:

             \(57 + 70 = 127\;(km)\) 

                            Đáp số: \(127km.\)

Bài 3

Tìm \(x\):

\(x + 42,31 = 29,1 \times 2\)

\(4,63 \times x + x \times 5,37 = 38\)

Phương pháp giải:

- Tính giá trị vế phải (nếu cần).

- Xác định vai trò của \(x\) và tìm \(x\) theo một số quy tắc sau:

+ Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.

+ Muồn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.

Lời giải chi tiết:

        \(\begin{array}{l}x + 42,31 = 29,1 \times 2\\x + 42,31 = 58,2\\x = 58,2 - 42,31\\x = 15,89\end{array}\)

        \(\begin{array}{l}4,63 \times x + x \times 5,37 = 38\\x \times (4,63 + 5,37) = 38\\x \times 10 = 38\\x = 38:10\\x = 3,8\end{array}\)

Bài 4

Mẹ đi chợ mua thịt và rau hết 240 000 đồng, số tiền mua rau bằng 60% số tiền mua thịt. Hỏi mẹ mua thịt hết bao nhiêu tiền, mua rau hết bao nhiêu tiền ?

Phương pháp giải:

- Đổi \(60\%  = \dfrac{{60}}{{100}} = \dfrac{3}{5}\). Khi đó ta có bài toán tìm hai số khi biết tổng và tỉ số của hai số đó. Theo bài số tiền mua rau bằng \(\dfrac{3}{5}\) số tiền mua thịt  nên ta vẽ sơ đồ biểu thị số tiền mua rau gồm 3 phần, số tiền mua thịt gồm \(5\) phần như thế. Ta tìm hai số theo công thức:

Số bé = (Tổng : tổng số phần bằng nhau) × số phần của số bé

hoặc

Số lớn =  (Tổng : tổng số phần bằng nhau) × số phần của số lớn.

Lời giải chi tiết:

Đổi \(60\%  = \dfrac{{60}}{{100}} = \dfrac{3}{5}\)

Ta có sơ đồ: 

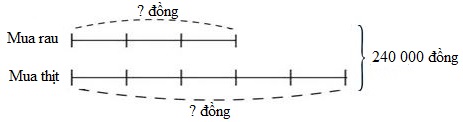
Theo sơ đồ, tổng số phần bằng nhau là:

          \(3 + 5 = 8\) (phần)

Mẹ mua thịt hết số tiền là:

        \(240 000 : 8 × 5 = 150 000\) (đồng)

Mẹ mua rau hết số tiền là:

       \(240 000 - 150 000 = 90 000\) (đồng)

              Đáp số: Mua thịt : \(150 000\) đồng;

                             Mua rau: \(90 000\) đồng.