Giải câu 5, 6, 7, 8, vui học trang 23, 24, 25

Bài 5

Viết vào ô trống (theo mẫu) :

Phương pháp giải:

Để đọc hoặc viết các số đo thể tích ta đọc hoặc viết số đo trước, sau đó đọc hoặc viết tên đơn vị đo thể tích.

Lời giải chi tiết:

Bài 6

Viết dấu (<, >, =) thích hợp vào ô trống:

a) 635,4352m³ ☐ 63 543 520cm³

b) \(\dfrac{{12345}}{{1000}}\)m³ ☐ 12,345m³

Phương pháp giải:

Đổi các số đo thể tích về cùng một đơn vị đo rồi so sánh kết quả với nhau.

Lời giải chi tiết:

a) Ta có: \(63\,\,543\,\,520c{m^3} = 63,54352{m^3}\)

    Mà \(63\,5,43\,52{m^3} > 63,54352{m^3}\)

    Vậy \(63\,5,43\,52{m^3} > 63\,\,543\,\,520{m^3}\).

b) Ta có: \(\dfrac{{12345}}{{1000}}{m^3} = 12,345{m^3}\)

    Mà \(12,345{m^3} = 12,345{m^3}\)

    Vậy \(\dfrac{{12345}}{{1000}}{m^3} = 12,345{m^3}\).

Bài 7

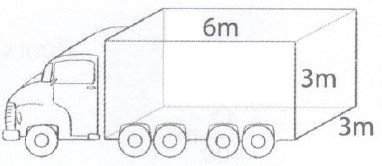
Một ô tô chở hàng có lòng thùng xe hình hộp chữ nhật kích thước như hình bên.

Người ta xếp các thùng hàng như nhau có dạng hình hộp chữ nhật có chiều dài bằng chiều rộng bằng 0,5m, chiều cao 1m lên xe đó. Hỏi xếp được bao nhiêu thùng hàng ? 

Phương pháp giải:

- Tính thể tích thùng xe và thể tích một thùng hàng theo công thức:

        Thể tích =  chiều dài × chiều rộng × chiều cao

- Tính số thùng hàng xếp được ta lấy thể tích thùng xe chia cho thể tích một thùng hàng.

Lời giải chi tiết:

Thể tích của thùng xe là:

           \(6 \times 3 \times 3 = 54\,\,({m^3})\)

Thể tích của một thùng hàng là:

           \(0,5 \times 0,5 \times 1 = 0,25\,\,({m^3})\)

Xếp được số thùng hàng là:

           \(54:0,25 = 216\) (thùng)

                        Đáp số: \(216\) thùng hàng.

Bài 8

a) Tính thể tích hình hộp chữ nhật có chiều dài 20cm, chiều rộng 12cm, chiều cao 17cm.

b) Tính thể tích hình lập phương cạnh \(\dfrac{3}{2}\)m.

Phương pháp giải:

- Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo).

- Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh.

Lời giải chi tiết:

a) Thể tích hình hộp chữ nhật đó là:

          \(20 \times 12 \times 17 = 4080\,\,(c{m^3})\)

b) Thể tích hình lập phương đó là:

           \(\dfrac{3}{2} \times \dfrac{3}{2} \times \dfrac{3}{2} = \dfrac{{27}}{8}\,({m^3})\)

                               Đáp số : a) \(4080cm^3\) ;

                                            b) \( \dfrac{{27}}{8}{m^3}\).

Vui học

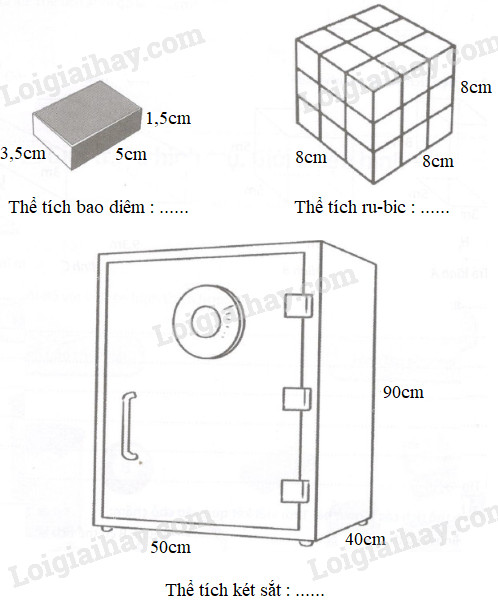
Một bao diêm hình hộp chữ nhật, một khối ru-bic hình lập phương và một két sắt hình hộp chữ nhật có kích thước như trong hình vẽ dưới đây. Tính rồi điền thể tích mỗi đồ vật vào chỗ chấm.

Phương pháp giải:

- Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo).

- Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh.

Lời giải chi tiết:

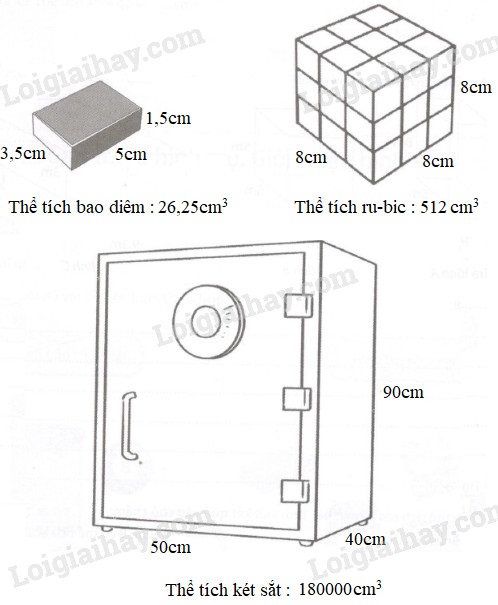
Thể tích bao diêm đó là:

           \(5 \times 3,5 \times 1,5 = 26,25\,\,(c{m^3})\)

Thể tích khối ru-bic đó là:

            \(8 \times 8 \times 8 = 512\,\,(c{m^3})\)

Thể tích két sắt đó là:

            \(50 \times 40 \times 90 = 180000\,\,(c{m^3})\) 

Vậy ta có kết quả như sau :