Giải Cùng em học Toán lớp 5 tập 1 - trang 5, 6 - Tuần 1 - Tiết 1

Bài 1

a) Viết phân số thích hợp chỉ phần tô đậm của mỗi hình sau vào chỗ chấm:

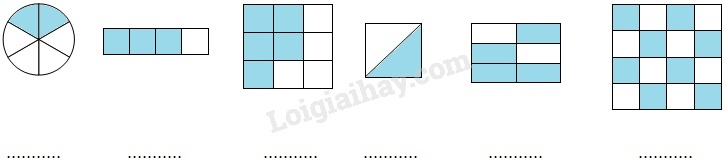
b) Tô màu vào hình vẽ cho thích hợp với phân số chỉ phần đã tô màu của mỗi hình sau:

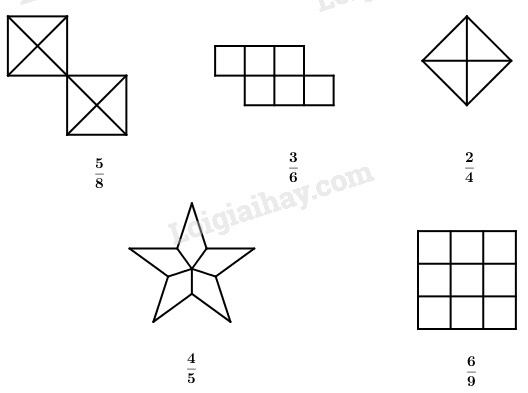
Phương pháp giải:

Quan sát hình vẽ, tìm số phần được tô màu và tổng số phần. Phân số chỉ phần đã tô màu có tử số là số phần được tô màu và mẫu số là tổng số phần.

Lời giải chi tiết:

a)

b)

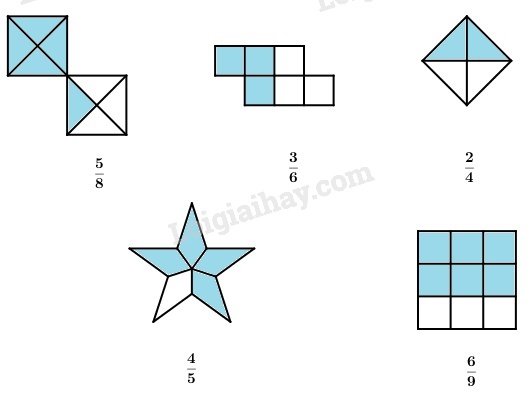
Bài 2

Viết phân số thích hợp vào ô trống

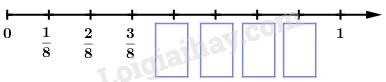
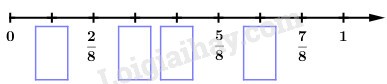
Phương pháp giải:

Quan sát trên tia số ta thấy 1 đơn vị được chia thành 8 phần bằng nhau, do đó mỗi phần nhỏ tương ứng với \(\dfrac{1}{8}\) đơn vị, từ đó ta điền được các phân số tương ứng trên tia số.

Lời giải chi tiết:

Bài 3

a) Viết các thương sau dưới dạng phân số:

\(3:13 = \dfrac{ \ldots }{ \ldots }\)

\(47:28 = \dfrac{ \ldots }{ \ldots }\)

\(2018:1000 = \dfrac{ \ldots }{ \ldots }\)

b) Viết các số tự nhiên sau dưới dạng phân số có mẫu số là 1:

\(7 = \dfrac{ \ldots }{ \ldots }\)

\(68 = \dfrac{ \ldots }{ \ldots }\)

\(403 = \dfrac{ \ldots }{ \ldots }\)

\(2018 = \dfrac{ \ldots }{ \ldots }\)

Phương pháp giải:

- Thương của phép chia số tự nhiên cho số tự nhiên (khác ) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.

- Mọi số tự nhiên có thể viết thành phân số có tử số là số tự nhiên đó và mẫu số bằng \(1\).

Lời giải chi tiết:

a) \(3:13 = \dfrac{3}{{13}}\);   

    \(47:28 = \dfrac{{47}}{{28}}\);

    \(2018:1000 = \dfrac{{2018}}{{1000}}\)

b) \(7 = \dfrac{7}{1}\);

    \(68 = \dfrac{{68}}{1}\); 

    \(403 = \dfrac{{403}}{1}\);

    \(2018 = \dfrac{{2018}}{1}\)

Bài 4

Rút gọn các phân số:

\(\begin{array}{l}\dfrac{{21}}{{27}} =  \ldots \\\dfrac{{125}}{{75}} =  \ldots \\\dfrac{{40}}{{140}} =  \ldots \\\dfrac{{756}}{{1000}} =  \ldots \end{array}\)

Phương pháp giải:

Khi rút gọn phân số có thể làm như sau:

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).

- Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Lời giải chi tiết:

\(\dfrac{{21}}{{27}} = \dfrac{{21:3}}{{27:3}} = \dfrac{7}{9}\)

\(\dfrac{{125}}{{75}} = \dfrac{{125:25}}{{75:25}} = \dfrac{5}{3}\)

\(\dfrac{{40}}{{140}} = \dfrac{{40:20}}{{140:20}} = \dfrac{2}{7}\)

\(\dfrac{{756}}{{1000}} = \dfrac{{756:4}}{{1000:4}} = \dfrac{{189}}{{250}}\)