Giải câu hỏi trang 66, 67, 68 SGK Toán 8 – Cánh diều

Hoạt động 1

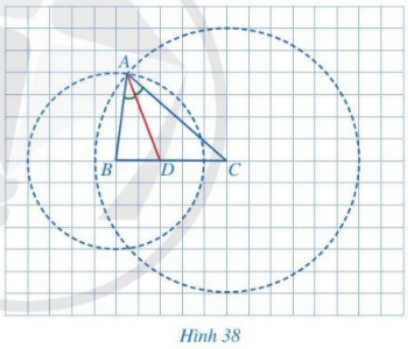
Trong Hình 38, tam giác ABC có AD là đường phân giác của góc BAC. Giả sử mỗi ô vuông của lưới ô vuông có độ dài cạnh bằng 1 cm.

a)      Tính độ dài các đoạn thẳng DB, DC.

b)     Tính độ dài các đoạn thẳng AB, AC.

c)      So sánh các tỉ số \(\frac{{DB}}{{DC}},\,\,\frac{{AB}}{{AC}}\).

Phương pháp giải:

a)      Đếm số ô tương ứng với các đoạn thẳng và tính độ dài.

b)     AB và AC là bán kính của hai đường tròn.

c)      Tính hai tỉ số và so sánh chúng.

Lời giải chi tiết:

a)      Ta thấy mỗi ô vuông có độ dài cạnh bằng 1cm.

Đoạn thẳng BD có độ dài bằng độ dài cạnh của 2 ô vuông nên BD dài 2 cm.

Đoạn thẳng DC có độ dài bằng độ dài cạnh của 3 ô vuông nên BD dài 3 cm.

b)     Ta thấy AB là bán kính đường tròn tâm B. Mà bán kính đường tròn tâm B có độ dài 4 ô vuông, tương ứng với 4 cm nên AB dài 4 cm.

Ta thấy AC là bán kính đường tròn tâm C. Mà bán kính đường tròn tâm C có độ dài 6 ô vuông, tương ứng với 6 cm nên AB dài 6 cm.

c)      Ta có: \(\frac{{DB}}{{DC}} = \frac{2}{3};\,\,\frac{{AB}}{{AC}} = \frac{4}{6} = \frac{2}{3}\)

Vậy \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\).

Luyện tập 1

Giải bài toán nêu trong phần mở đầu.

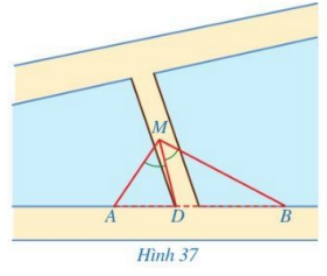
Bài toán: Một người đứng ở vị trí M trên cây cầu bắc qua con kênh quan sát ba điểm thẳng hàng A, B, D lần lượt là chân hai cột đèn trồng ở bờ kênh và chân cầu (Hình 37). Người đó nhận thấy góc nhìn đến hai điểm A, D thì bằng góc nhìn đến hai điểm B, D, tức là \(\widehat {AMD} = \widehat {BMD}\). Người đó muốn ước lượng tỉ số khoảng cách từ vị trí M đang đứng đến điểm A và đến điểm B mà không cần phải đo trực tiếp hai khoảng cách đó. Có thể ước lượng tỉ số đó được hay không?

Phương pháp giải:

Dựa vào tính chất đường phân giác để chứng minh.

Lời giải chi tiết:

Khoảng cách từ M đến A là đoạn MA.

Khoảng cách từ M đến B là đoạn MB.

Vì \(\widehat {AMD} = \widehat {BMD}\) nên MD là đường phân giác của tam giác MAB.

Ta có: \(\frac{{MA}}{{MB}} = \frac{{DA}}{{DB}}\) (Tính chất đường phân giác trong tam giác)

Vậy người đó có thể ước lượng tỉ số MA và MB bằng cách đó và tính tỉ số giữa DA và DB mà không cần phải đo trực tiếp hai khoảng cách MA và MB.

Luyện tập 2

Cho tam giác ABC có \(AB < AC\), AD là đường phân giác. Chứng minh \(DB < DC\).

Phương pháp giải:

Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài.

Lời giải chi tiết:

Xét tam giác ABC có AD là đường phân giác nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\)

Mà \(AB < AC\)\( \Rightarrow \frac{{AB}}{{AC}} < 1 \Rightarrow \frac{{DB}}{{DC}} < 1 \Rightarrow DB < DC\).

Luyện tập 3

Cho tam giác ABC có ba đường phân giác AD, BE, CF. Chứng minh \(\frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = 1\)

Phương pháp giải:

Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài.

Lời giải chi tiết:

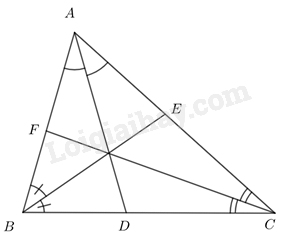
Xét tam giác ABC với ba đường phân giác AD, BE, CF, ta có:

\(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}};\,\,\frac{{BC}}{{BA}} = \frac{{EC}}{{EA}};\,\,\frac{{CA}}{{CB}} = \frac{{FA}}{{FB}}\) (Tính chất đường phân giác)

\( \Rightarrow \frac{{DB}}{{DC}}.\frac{{EC}}{{EA}}.\frac{{FA}}{{FB}} = \frac{{AB}}{{AC}}.\frac{{BC}}{{BA}}.\frac{{CA}}{{CB}} = \frac{{AB.BC.CA}}{{CA.AB.BC}} = 1\) (đpcm).

Luyện tập 4

Cho tam giác ABC, điểm D thuộc cạnh BC sao cho \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\). Chứng minh AD là tia phân giác của góc BAC.

Phương pháp giải:

Dựa vào tính chất đường phân giác để chứng minh yêu cầu đề bài.

Lời giải chi tiết:

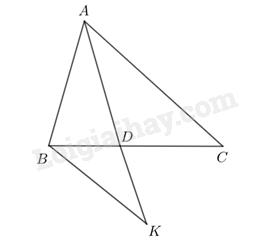
Từ B kẻ đường thẳng song song với AC, cắt AD tại K.

Vì \(BK//AC\) nên theo hệ quả của định lý Thales, ta có: \(\frac{{DB}}{{DC}} = \frac{{BK}}{{AC}}\)

Mà \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) nên \(\frac{{BK}}{{AC}} = \frac{{AB}}{{AC}} \Rightarrow AB = BK\)

Khi đó tam giác ABK cân tại B nên \(\widehat {BAK} = \widehat {BKA}\)

Mà \(BK//AC\) nên \(\widehat {BKA} = \widehat {KAC}\)

\( \Rightarrow \widehat {BAK} = \widehat {KAC}\)

Vậy AD là đường phân giác trong tam giác ABC.