Giải câu hỏi trang 50, 51, 52 SGK Toán 9 tập 2 - Cùng khám phá
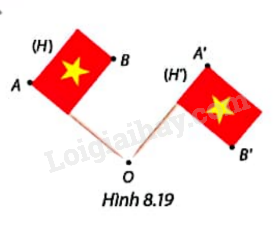
Trong Hình 8.19, Lá cờ (H) được quay quanh điểm O theo chiều kim đồng hồ đến vị trí mới (H’). a) So sánh độ dài OA và OA’, OB và OB’. b) So sánh số đo \(\widehat {AOA'}\) và \(\widehat {BOB'}\).
HĐ
Trả lời câu hỏi Hoạt động trang 50 SGK Toán 9 Cùng khám phá
Trong Hình 8.19, Lá cờ (H) được quay quanh điểm O theo chiều kim đồng hồ đến vị trí mới (H’).
a) So sánh độ dài OA và OA’, OB và OB’.
b) So sánh số đo \(\widehat {AOA'}\) và \(\widehat {BOB'}\).
Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
a) Ta có OA = OA’ , OB = OB’.
b) \(\widehat {AOA'}\)= \(\widehat {BOB'}\).
LT1
Trả lời câu hỏi Luyện tập 1 trang 50 SGK Toán 9 Cùng khám phá
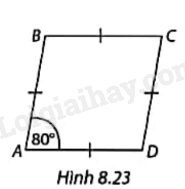
Cho hình thoi ABCD có \(\widehat A = {80^o}\) như Hình 8.23.
a) Tìm ảnh của điểm D qua phép quay ngược chiều \({80^o}\) tâm A.
b) Phép quay thuận chiều \({100^o}\) tâm B biến điểm C thành điểm nào?
Phương pháp giải:
Phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm A’ thuộc đường tròn (O;OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OA’ thì điểm A tạo nên cung AmA’ có số đo \({\alpha ^o}\)
(Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O).
Lời giải chi tiết:
a) Xét hình thoi ABCD, ta có \(\widehat {DAB} = {80^o}\), suy ra B là ảnh của D qua phép quay ngược chiều \({80^o}\)tâm A.
b) Ta có \(\widehat {CBA} = \widehat {CDA} = \frac{{{{360}^o} - {{2.80}^o}}}{2} = {100^o}\)
Vậy phép quay thuận chiều \({100^o}\) tâm B biến điểm C thành điểm A.
LT2
Trả lời câu hỏi Luyện tập 2 trang 53 SGK Toán 9 Cùng khám phá
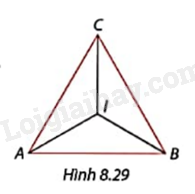
Trong Hình 8.29, tam giác ABC đều và \(\widehat {AIB} = \widehat {BIC} = \widehat {AIC} = {120^o}\). Tìm hai phép quay tâm I giữ nguyên tam giác đều ABC.
Phương pháp giải:
Phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm A’ thuộc đường tròn (O;OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OA’ thì điểm A tạo nên cung AmA’ có số đo \({\alpha ^o}\)
(Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O).
Lời giải chi tiết:
Ta có \(\widehat {AIB} = \widehat {BIC} = \widehat {AIC} = {120^o}\). Các phép quay thuận chiều (hoặc ngược chiều) 120o , 240o, 360o tâm I giữ nguyên tam giác đều ABC.
VD
Trả lời câu hỏi Vận dụng trang 53 SGK Toán 9 Cùng khám phá
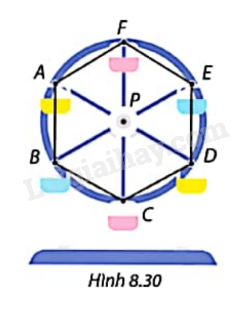
Một vòng quay có 6 cabin tại vị trí các đỉnh của một lục giác đều ABCDEF như Hình 8.30. Vòng quay này quay theo chiều quay kim đồng hồ. Tìm một phép quay tâm P (P là vị trí trục của vòng quay) để:
a) Cabin ở vị trí A di chuyển đến vị trí E. Khi đó cabin ở vị trí E di chuyển đến vị trí nào?
b) Cabin ở vị trí A di chuyển đến vị trí D. Tìm ảnh của các đỉnh còn lại của lục giác đều ABCDEF qua phép quay này và rút nhận xét.
Phương pháp giải:
Phép quay thuận chiều \({\alpha ^o}({0^o} < {\alpha ^o} < {360^o})\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm A’ thuộc đường tròn (O;OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OA’ thì điểm A tạo nên cung AmA’ có số đo \({\alpha ^o}\)
(Định nghĩa tương tự cho phép quay ngược chiều \({\alpha ^o}\) tâm O).
Lời giải chi tiết:
Ta có AF = FE = ED = DC = CB = BA nên số đo các cung nhỏ AF, FE, ED, DC, CB, BA đều bằng \(\frac{{{{360}^o}}}{6} = {60^o}\)
a) Vậy phép quay theo chiều kim đồng hồ 120o tâm P biến vị trí điểm A đến vị trí điểm E. Khi đó cabin ở vị trí E di chuyển đến vị trí C.
b) Cabin ở vị trí A di chuyển đến vị trí D tạo thành phép quay 180o.
Vị trí F di chuyển đến vị trí C
Vị trí E di chuyển đến vị trí B
Vị trí D di chuyển đến vị trí A
Vị trí C di chuyển đến vị trí F
Vị trí B di chuyển đến vị trí E.
Nhận xét: Lục giác đều ABCDEF quay một vòng 180o.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải câu hỏi trang 50, 51, 52 SGK Toán 9 tập 2 - Cùng khám phá timdapan.com"