Giải bài tập 9.16 trang 85 SGK Toán 9 tập 2 - Cùng khám phá
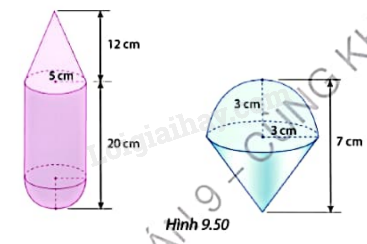
Tính thể tích của mỗi hình ở Hình 9.50.
Đề bài
Tính thể tích của mỗi hình ở Hình 9.50.
Phương pháp giải - Xem chi tiết
Thể tích hình nón là: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón).
Thể tích hình trụ là: \(V = \pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình trụ).
Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\)(với R là bán kính hình cầu)
Lời giải chi tiết
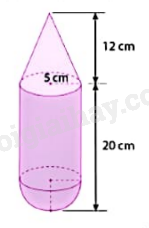
Thể tích phần hình nón là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.5^2}.12 = 100\pi \) (cm3)
Thể tích phần hình trụ cao 20 cm là :
\(V = \pi {r^2}h = \pi {.5^2}.20 = 500\pi \) (cm3)
Thể tích phần hình cầu là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.5^3} = \frac{{500}}{3}\pi \) (cm3)
Thể tích phần hình trụ là:
\(500\pi - \frac{{500}}{3}\pi = \frac{{1000}}{3}\pi \) (cm3)
Vậy thể tích hình trên là:
\(100\pi + \frac{{500}}{3}\pi + \frac{{1000}}{3}\pi = 600\pi \) (cm3)
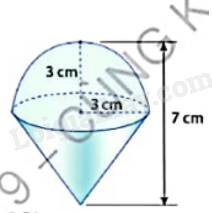
Thể tích hình nón chiều cao 7 cm là:
\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{2}\pi {.3^2}.7 = 31,5\pi \) (cm3)
Thể tích nửa hình cầu là:
\(\frac{V}{2} = \frac{{\frac{4}{3}\pi {R^3}}}{2} = 18\pi \) (cm3)
Thể tích phần hình nón là:
\(31,5\pi - 18\pi = 13,5\pi \) (cm3)
Thể tích hình trên là:
\(13,5\pi + 18\pi = 31,5\pi \) (cm3)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 9.16 trang 85 SGK Toán 9 tập 2 - Cùng khám phá timdapan.com"