Giải bài tập 4.30 trang 82 SGK Toán 9 tập 1 - Kết nối tri thức
Đố vui. Chu vi Trái Đất bằng bao nhiêu? Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau: 1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng. 2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-l
Đề bài
Đố vui. Chu vi Trái Đất bằng bao nhiêu?
Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:
1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng.
2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-lếch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy 1 tháp cao 25 m có bóng trên mặt đất dài 3,1 m.
Từ hai quan sát trên, ông có thể tính xấp xỉ “chu vi” của Trái Đất như thế nào? (trên Hình 4.38), điểm O là tâm của Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB.
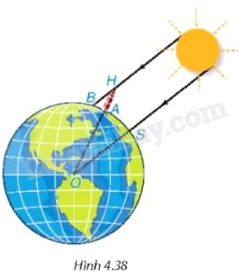
Phương pháp giải - Xem chi tiết
Vẽ hình minh họa để dễ quan sát.
Dựa vào quan sát thứ nhất ta có \(SO \bot SB\) nên \(\Delta SOB\) vuông tại S.
Dựa vào quan sát thứ hai, ta tính được \(\widehat {BHA} \) và chứng minh được BH // OS nên \(\widehat {BHA} = \widehat {AOS}\).
Dựa vào tỉ số lượng giác của các góc để trong tam giác OAS để tính bán kính OA của Trái Đất.
Từ đó sử dụng công thức tính chu vi hình tròn để tính chu vi Trái Đất.
Lời giải chi tiết
Ta có hình minh họa các điểm để dễ quan sát như sau:
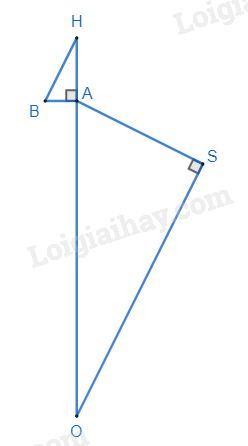
Qua quan sát thứ nhất, vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng, do đó \(SO \bot SB\) nên \(\Delta SOB\) vuông tại S.
Qua quan sát thứ hai, Eratosthenes thấy 1 tháp cao 25m có bóng trên mặt đất dài 3,1m
Ta có HA là chiều cao của tháp nên HA = 25m, HB là tia sáng mặt trời nên tạo ra bóng của tháp trên mặt đất là AB = 3,1m.
Xét tam giác HBA vuông tại A nên \(\tan \widehat {BHA} = \frac{{BA}}{{HA}} = \frac{{3,1}}{{25}} = 0,124\), suy ra \(\widehat {BHA} \approx 7,{1^0}\).
Mà các tia nắng mặt trời chiếu cùng một góc và cùng 1 thời điểm trong ngày nên các tia sáng BH và OS song song với nhau (BH // OS).
Khi đó ta có: \(\widehat {BHA} = \widehat {AOS}\) (hai góc so le trong). Do đó \(\widehat {AOS} \approx 7,{1^0}\).
Ta có khoảng cách của thành phố Alexandria và Syene là 800km nên AS = 800km.
Xét tam giác OAS vuông tại S nên ta có:
\(\sin \widehat {AOS} = \frac{{AS}}{{OA}}\) suy ra \(OA = \frac{{AS}}{{\sin \widehat {AOS}}} \approx \frac{{800}}{{\sin 7,{1^0}}} \approx 6472\left( {km} \right)\)
Vì OA là bán kính Trái Đất nên ta tính được chu vi Trái Đất là:
\(C = 2\pi .OA \approx 2\pi .6472 \approx 40665\left( {km} \right)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 4.30 trang 82 SGK Toán 9 tập 1 - Kết nối tri thức timdapan.com"







