Bài III.11, III.12 trang 53,54 SBT Vật lí 10
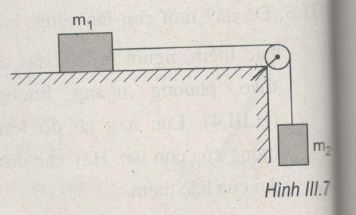
Giải bài III.11, III.12 trang 53,54 sách bài tập vật lý 10. Một vật có khối lượng m1 =3,0 kg được đặt trên một mặt bàn nằm ngang, nhẵn. Vật được nối với một vật khác có khối lượng m2 = 1,0 kg nhờ một sợi dây không dãn vắt qua một ròng rọc gắn ở mép bàn (H.III.7). Lấy g = 9,8 m/s2.
III.11.
Một vật có khối lượng m1 =3,0 kg được đặt trên một mặt bàn nằm ngang, nhẵn. Vật được nối với một vật khác có khối lượng m2 = 1,0 kg nhờ một sợi dây không dãn vắt qua một ròng rọc gắn ở mép bàn (H.III.7). Lấy g = 9,8 m/s2.
a) Tính gia tốc của mỗi vật.
b) Nếu lúc đầu vật m1 đứng yên cách mép bàn 150 cm thì sau bao lâu sau nó sẽ đến mép bàn.
c) Tính lực căng của dây.
Phương pháp giải:
- Áp dụng định luật III Niuton: Trong mọi trường hợp, khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng lại vật A một lực. Hai lực này có cùng giá, cùng độ lớn, nhưng ngược chiều.
- Áp dụng định luật II Niuton: F = m.a
Lời giải chi tiết:
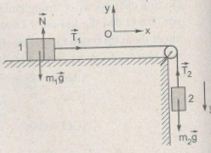
Chọn chiều dương là chiều chuyển động của dây (H.III.8G)
a. Xét vật 1:
Oy: N – m1g = 0
Ox: \(a = \displaystyle{{{T_1}} \over {{m_1}}}\) (1)
Xét vật 2
Oy: m2a = m2g – T2 (2)
Theo định luật III Niu-tơn:
T1 = T2 = T (3)
Từ (1), (2) và (3) suy ra
\(a = \displaystyle{{{m_2}g} \over {{m_1} + {m_2}}} = {{1,0.9,8} \over {3,0 + 1,0}} \\= 2,45 \approx 2,5(m/{s^2})\)
b. \(s = \displaystyle{1 \over 2}a{t^2} \\= > t = \displaystyle\sqrt {{{2s} \over a}} = \sqrt {{{2.1,50} \over {2,45}}} = 1,1(s)\)
c. Từ (2) và (3)
T = m2(g – a) = 1,0(9,8 – 2,45) = 7,35 N
III.12.
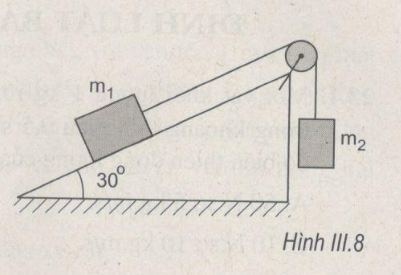
Một vật có khối lượng m1 =3,7 kg nằm trên một mặt không ma sát, nghiêng 30° so với phương ngang. Vật được nối với một vật thứ hai có khối lượng m2 = 2,3 kg bằng một sợi dây không dãn vắt qua một ròng rọc gắn ở đỉnh của mặt phẳng nghiêng (H.III.8).Cho g = 9,8 m/s2.
a) Tính gia tốc và hướng chuyển động của mỗi vật.
b) Tính lực căng của dây.
Lời giải chi tiết:
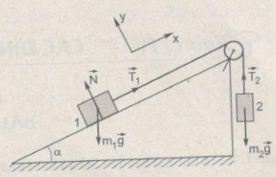
a. Chọn chiều dương của hệ tọa độ cho mỗi vật như hình vẽ
* Xét vật 1:
Oy: N – m1gcosα = 0
Ox: T1 – m1gsinα = m1a (1)
* Xét vật 2:
Mm2g – T2 = m2a (2)
T1 = T2 = T (3)
Từ (1), (2) và (3) suy ra:
\(a = \displaystyle{{({m_2} - {m_1}sin\alpha )g} \over {{m_1} + {m_2}}} \\= \displaystyle{{(2,30 - 3,70.0,5)9,8} \over {2,30 + 3,70}} \\= 0,735(m/{s^2})\)
a > 0: vật m2 đi xuống và vật m1 đi lên.
b. Từ (2) và (3) suy ra:
T = m2(g – a) = 2,30(9,8 – 0,735)
= 20,84 N.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài III.11, III.12 trang 53,54 SBT Vật lí 10 timdapan.com"