Giải Bài 9.9 trang 50 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho tam giác ABC cân tại A và một điểm M tuỳ ý thuộc đoạn thẳng BC. Chứng minh rằng tổng khoảng cách từ điểm M đến đường thẳng AB, AC là một số không đổi
Đề bài
Cho tam giác ABC cân tại A và một điểm M tuỳ ý thuộc đoạn thẳng BC. Chứng minh rằng tổng khoảng cách từ điểm M đến đường thẳng AB, AC là một số không đổi
Phương pháp giải - Xem chi tiết
- Xét khi M trùng B, C và khi M khác B, C
- Kẻ \(MP \bot AC;MQ \bot AB\)
-Chứng minh: \(\Delta RBM\) cân tại R
-Chứng minh: MP + MQ = BS + SI = BI = CK.
Lời giải chi tiết
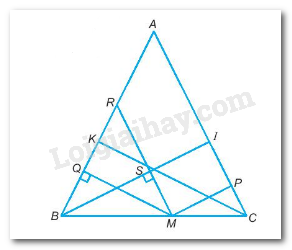
TH1:Khi M trùng với B hay C thì tổng khoảng cách đó là BI hoặc CK
Theo bài 9.8: BI = CK
TH2: Khi M khác B, khác C
Kẻ \(MP \bot AC;MQ \bot AB\)
\( \Rightarrow \)Tổng khoảng cách đang xét: MQ + MP
Qua M kẻ \(MR // AC\); MR cắt BI tại S.
\( \Rightarrow \widehat C = \widehat {RMB}\) (2 góc đồng vị)
Mà \(\widehat C = \widehat B\)
\( \Rightarrow \widehat B = \widehat {RMB}\)
\( \Rightarrow \Delta RBM\) cân tại R
MQ là khoảng cách từ M đến RB, BS là khoảng cách từ B đến RM
Theo bài 9.8: MQ = BS
Ta có: MR // AC, MP và SI có độ dài là khoảng cách giữa hai đường thẳng đó nên MP = SI
Suy ra: MP + MQ = BS + SI = BI = CK.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Bài 9.9 trang 50 sách bài tập toán 7 - Kết nối tri thức với cuộc sống timdapan.com"







