Giải bài 8.20 trang 57 SGK Toán 6 Kết nối tri thức với cuộc sống

Cho ba điểm A, B, C cùng nằm trên đường thẳng d sao cho B nằm giữa A và C. Hai điểm D và E không thuộc d và không cùng thẳng hàng với điểm nào trong các điểm A , B và C.

Câu a

Có bao nhiêu đường thẳng, mỗi đường thẳng đi qua ít nhất hai trong năm điểm đã cho?

Phương pháp giải:

- Kẻ đường thẳng DE.

- Tìm các đường thẳng đi qua D và 1 điểm trên d, các đường thẳng đi qua E và 1 điểm trên d.

Lời giải chi tiết:

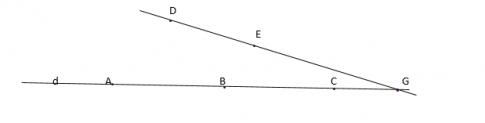
Ta cần tìm các đường thẳng đi qua 5 điểm A, B, C, D, E.

Ta đã có 2 đường thẳng là DE và d (đường thẳng đi qua A, B, C).

Đường thẳng đi qua D và 1 điểm trên d là: DA, DB, DC.

Đường thẳng đi qua E và 1 điểm trên d là: EA, EB, EC.

Vậy có 8 đường thẳng  đi qua ít nhất hai trong năm điểm đã cho: DE, d, DA, DB, DC, EA, EB, EC.

Câu b

Tìm trên đường thẳng d điểm G sao cho ba điểm D, E, G thẳng hàng. Có phải khi nào cũng tìm được điểm G như thế hay không?

Phương pháp giải:

- Điểm G là điểm chung của hai đường thẳng.

- Hai đường thẳng không có điểm chung là hai đường thẳng song song.

Lời giải chi tiết:

Ta cần tìm điểm G nằm trên d và D, E, G thẳng hàng. Khi đó G là điểm chung của DE và d. Hay G là giao điểm của DE và d.

Không phải khi nào cũng tìm được điểm G như thế này, điểm G tồn tại khi đường thẳng DE cắt d. Khi DE và d song song với nhau thì không tồn tại điểm G.