Bài 8 trang 91 Vở bài tập toán 9 tập 2

Đề bài

Chứng minh rằng trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau. 

Lời giải chi tiết

a) Trường hợp tâm đường tròn nằm ngoài hai dây song song 

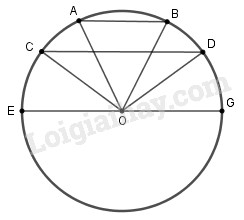
Giả sử \(AB//CD.\)

Kẻ đường kính \(EG//CD\)  và nối các điểm \(A,B,C,D\) với tâm \(O.\) Khi đó, ta có \(\Delta OAB\) cân vì \(OA = OB\) 

Suy ra \(\widehat A = \widehat B.\) (1)

Mặt khác, \(\widehat A = \widehat {AOE}\) và \(\widehat B = \widehat {BOG},\) (2) vì \(AB//EG\) (cùng song song với \(CD)\)

Từ (1) và (2) \( \Rightarrow \widehat {AOE} = \widehat {BOG}.\)

Do đó, ta có :

sđ\(\overparen{AE}\) =sđ \(\overparen{BG}\)      (3)

Chứng minh tương tự, ta có \(sđ\overparen{CE}=sđ\overparen{DG}\)      (4)

Vì \(C\) nằm trên cung \(AE,\) \(D\) nằm trên cung \(BG\) nên ta có :

sđ\(\overparen{AC}\) = sđ\(\overparen{AE}\) - sđ\(\overparen{CE}\)

và sđ\(\overparen{BD}\) = sđ\(\overparen{BG}\) - sđ\(\overparen{DG}\)

Vậy từ (3) và (4) ta có  :

sđ\(\overparen{AC}\) = sđ\(\overparen{BD}\)\( \Rightarrow \) \(\overparen{AC}\) = \(\overparen{BD}\) (đpcm)

b) Trường hợp tâm đường tròn nằm trong hai dây song song 

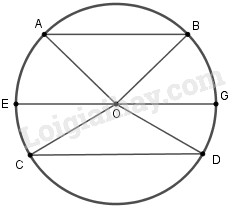
Kẻ đường kính \(EG//CD\) và nối các điểm \(A,B,C,D\) với tâm \(O.\)

Chứng minh tương tự câu a) , ta có :

sđ\(\overparen{AE}\) = sđ \(\overparen{BG}\) và sđ\(\overparen{EC}\) =sđ \(\overparen{GD}\) (5)

Vì \(E\) nằm trên cung \(AC,\) \(G\) nằm trên cung \(BD\) và từ \(\left( 4 \right)\) nên ta có :

sđ\(\overparen{AC}\) = sđ\(\overparen{AE}\) + sđ\(\overparen{EC}\)

và sđ\(\overparen{BD}\) = sđ\(\overparen{BG}\) + sđ\(\overparen{GD}\) 

\( \Rightarrow \) sđ\(\overparen{AC}\) = sđ \(\overparen{BD}\) hay \(\overparen{AC}\) = \(\overparen{BD}\) (đpcm)