Bài 7 trang 90 Vở bài tập toán 9 tập 2
Giải bài 7 trang 90 VBT toán 9 tập 2. Cho hai đường tròn bằng nhau (O) và (O’) cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO’D. Gọi E là giao điểm thứ hai của AO với đường tròn (O’)...
Đề bài
Cho hai đường tròn bằng nhau (O) và (O’) cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO’D. Gọi E là giao điểm thứ hai của AO với đường tròn (O’)
a) So sánh các cung nhỏ BC, BD
b) Chứng minh rằng B là điểm chính giữa của cung EBD (tức là điểm B chia cung EBD thành hai cung bằng nhau: \(\overparen{BE}=\overparen{BD}\))
Phương pháp giải - Xem chi tiết
* Chứng minh hai tam giác bằng nhau hoặc tam giác cân để suy ra hai dây bằng nhau.
Từ đó sử dụng định lý: Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+) Hai cung bằng nhau căng hai dây bằng nhau.
+) Hai dây bằng nhau căng hai cung bằng nhau.
Lời giải chi tiết
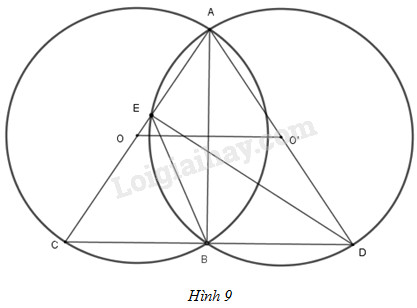
a) Nối \(AB\) (xem hình 9)
\(\Delta ABC\) và \(\Delta ABD\) là hai tam giác vuông bằng nhau vì hai tam giác có chung cạnh \(AB\) và \(AC = AD\) (đường kính)
Suy ra \(BC = BD\) hay \(\overparen{BD}>\overparen{BC}\) vì \(\left( O \right)\) và \(\left( {O'} \right)\) là hai đường tròn bằng nhau.
b) Xét \(\Delta ECD,\) vì \(E\) nằm trên đường tròn và đường kính \(AO'D\) nên \(\widehat {AED} = 90^\circ .\)
Suy ra \(\widehat {CED} = 90^\circ .\) Vậy \(\Delta ECD\) vuông tại \(E.\)
Theo kết quả câu a) ta có \(BC = BD.\)
Do đó, \(BE\) là đường trung tuyến của \(\Delta ECD \Rightarrow BE = BD.\) Vậy ta có \(\overparen{BD}>\overparen{BC}\) hay \(B\) là điểm chính giữa của cung \(EBD.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 7 trang 90 Vở bài tập toán 9 tập 2 timdapan.com"







