Bài 58 trang 136 Vở bài tập toán 8 tập 1

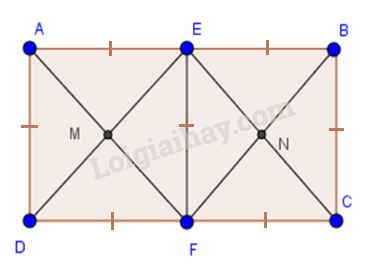
Cho hình chữ nhật \(ABCD\) có \(AB = 2AD\).  Gọi \(E, F\) theo thứ tự là trung điểm của \(AB, CD\). Gọi \(M\) là giao điểm của \(AF\) và \(DE\), \(N\) là giao điểm của \(BF\) và \(CE\). 

LG a

 Tứ giác \(ADFE\) là hình gì? Vì sao?

Phương pháp giải:

Áp dụng dấu hiệu nhận biết:

- Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành,

- Tứ giác có các cặp cạnh đối song song là hình bình hành,

- Hình bình hành có một góc vuông là hình chữ nhật,

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Giải chi tiết:

Hình chữ nhật \(ABCD\) có \(AE=EB, DF=FE\) và \(AB=2AD\) nên 

\(AE=EB=BC=CF=DF=AD\) 

Tứ giác \(ADFE\) có \(AE // DF\) và \(AE = DF\) nên là hình bình hành.

Hình bình hành \(ADFE\) có \(\widehat{A} = 90^0\) nên là hình chữ nhật.

Hình chữ nhật \(ADFE\) có \(AE = AD\) nên là hình vuông.

LG b

 Tứ giác \(EMFN\) là hình gì? Vì sao?  

Phương pháp giải:

Áp dụng dấu hiệu nhận biết:

- Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành,

- Tứ giác có các cặp cạnh đối song song là hình bình hành,

- Hình bình hành có một góc vuông là hình chữ nhật,

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Giải chi tiết:

 Xét tứ giác \(DEBF\) có \(EB // DF\) và \( EB = DF\) nên là hình bình hành, suy ra \(DE // BF\)

Chứng minh tương tự ta có \(AF // EC\)

Tứ giác \(EMFN\) có \(ME//FN\) và \(MF // EN\) nên là hình bình hành.

Ta có \(ME=MF\) và \(ME \bot MF\) vì \(ADFE\) là hình vuông (câu a).

Hình bình hành \(EMFN\) có \(\widehat{M} = 90^0\) nên là hình chữ nhật.

Hình chữ nhật \(EMFN\) có \(ME = MF\) nên là hình vuông.

Giải thích: \(AF // EC\) 

Xét tứ giác \(AECF\) có \(EA // CF, EA = CF\) nên \(AECF\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

\( \Rightarrow \) \(AF // EC\) (tính chất hình bình hành)