Bài 5.5, 5.6 trang 14 SBT Vật Lí 12

5.5

Hai dao động điều hòa cùng phương, cùng chu kì có phương trình lần lượt là \({x_1} = 4c{\rm{os(4}}\pi {\rm{t + }}\dfrac{\pi }{2})(cm)\) và \({x_2} = 3c{\rm{os(4}}\pi {\rm{t + }}\pi )(cm)\). Biên độ và pha ban đầu của dao động tổng hợp là

A. \(5cm;36,{9^0}\)

B. \(5cm;0,7\pi \left( {ra{\rm{d}}} \right)\)

C. \(5cm;0,2\pi \left( {ra{\rm{d}}} \right)\)

D. \(5cm;0,3\pi \left( {ra{\rm{d}}} \right)\)

Phương pháp giải:

Vận dụng công thức tổng hợp dao động điều hòa: \({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi\)

Lời giải chi tiết: 

\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi  = {4^2} + {3^2} + 2.4.3.\cos (\pi  - \dfrac{\pi }{2}) = 25\\ \Rightarrow A = 5cm\end{array}\)

Ta có giản đồ Fre-nen:

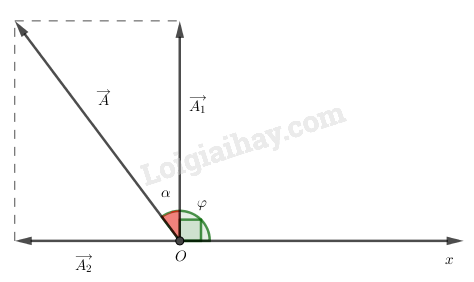
Từ hình vẽ ta thấy: \(\tan \alpha  = \dfrac{{{A_2}}}{{{A_1}}} = \dfrac{3}{4} \Rightarrow \alpha  = 0,2\pi  \Rightarrow \varphi  = \alpha  + \dfrac{\pi }{2} = 0,7\pi (rad)\)

Chọn B

5.6

Hai dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là \({x_1} = 5c{\rm{os(}}\dfrac{\pi }{2}{\rm{t + }}\dfrac{\pi }{4})(cm)\); \({x_2} = 5c{\rm{os(}}\dfrac{\pi }{2}{\rm{t + }}\dfrac{{3\pi }}{4})(cm)\). Biên độ và pha ban đầu của dao động tổng hợp là

A.\(5cm;\dfrac{\pi }{2}(ra{\rm{d}})\)

B. \(7,1cm;0(ra{\rm{d}})\) 

C. \(7,1cm;\dfrac{\pi }{2}(ra{\rm{d}})\)

D. \(7,1cm;\dfrac{\pi }{4}(ra{\rm{d}})\)

Phương pháp giải:

Vận dụng công thức tổng hợp dao động điều hòa: \({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi\)

Lời giải chi tiết: 

\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi  = {5^2} + {5^2} + 2.5.5.\cos (\dfrac{{3\pi }}{4} - \dfrac{\pi }{4}) = 50\\ \Rightarrow A = 5\sqrt 2 cm\end{array}\)

Ta có giản đồ Fre-nen:

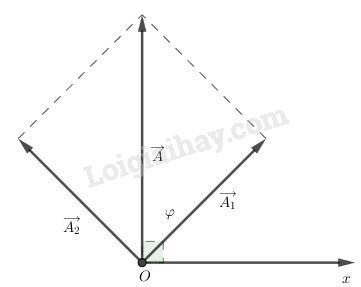
\(\varphi  = \dfrac{\pi }{2}rad\)

Chọn C