Câu 50.1, 50.2, 50.3, 50.4, 50.5, 50.6 phần bài tập trong SBT – Trang 139,140 Vở bài tập Vật lí 9

50.1.

Có thể dùng kính lúp để quan sát vật nào dưới đây?

A. Một ngôi sao.           B. Một con vi trùng.

C. Một con kiến.           D. Một bức tranh phong cảnh.

Phương pháp: Kính lúp là thấu kính hội tụ có tiêu cự ngắn, dùng để quan sát các vật nhỏ.

Lời giải chi tiết:

Ta có: Kính lúp là thấu kính hội tụ có tiêu cự ngắn, dùng để quan sát các vật nhỏ.

=> Trong các vật ở trên, kính lúp dùng để quan sát một con kiến.

Chọn C.

50.2.

Thấu kính nào dưới đây có thể dùng làm kính lúp ?

A. Thấu kính phân kì có tiêu cự 10 cm.

B. Thấu kính phân kì có tiêu cự 50 cm.

C. Thấu kính hội tụ có tiêu cự 10 cm.

D. Thấu kính hội tụ có tiêu cự 50 cm.

Phương pháp: Kính lúp là thấu kính hội tụ có tiêu cự ngắn

Lời giải chi tiết: 

Ta có: Kính lúp là thấu kính hội tụ có tiêu cự ngắn

=> Trong các thấu kính trên, thấu kính dùng làm kính lúp là thấu kính hội tụ có tiêu cự 10 cm.

Chọn C.

50.3.

Khi quan sát một vật nhỏ qua kính lúp, ta nhìn thấy ảnh của vật hay nhìn trực tiếp thấy vật? Có thể làm thí nghiệm đơn giản nào để để chứng minh câu trả lời của em là đúng?

Phương pháp: Vận dụng tính chất ảnh của vật qua thấu kính hội tụ

Lời giải chi tiết:

Khi quan sát một vật nhỏ qua kính lúp, ta nhìn thấy ảnh của vật.

Để kiếm tra, có thể dùng kính để quan sát một chiếc bút chì được nhìn qua kính, phần còn lại nằm ngoài kính. Khi đó phần nhìn qua kính lớn hơn, còn phần nằm ngoài kính thì nhỏ hơn. Như vậy có thể nhìn thấy ảnh của bút chì qua kính.

50.4.

Dùng kính lúp có số bội giác 2x và kính lúp có số bội giác 3x để quan sát cùng một vật và với cùng điều kiện thì trong trường hợp nào ta sẽ thấy ảnh lớn hơn ? Trong hai kính đó, kính nào có tiêu cự dài hơn?

Phương pháp: 

- Dùng kính lúp có số bội giác càng lớn để quan sát thì ta thấy ảnh càng lớn.

- Hệ thức giữa số bội giác G và tiêu cự f (đo bằng đơn vị xentimet) của một kính lúp: \(G = \displaystyle{{25} \over f}\)

Lời giải chi tiết:

Dùng kính lúp có số bội giác 3x ta sẽ thấy ảnh lớn hơn khi dùng kính có số bội giác 2x khi qua sát cùng một vật trong cùng một điều kiện quan sát.

Kính có số bộ giác 2x sẽ có tiêu cự dài hơn vì \(G = \displaystyle{{25} \over f}\) nên G và f tỉ lệ nghịch

50.5.

Một người dùng kính lúp có tiêu cự 10 cm để quan sát một vật nhỏ. Vật đặt cách kính 8 cm.

a. Dựng ảnh của vật qua kính, không cần đúng tỉ lệ.

b. Ảnh là ảnh thật hay ảnh ảo ?

c. Ảnh lớn hơn hay nhỏ hơn vật bao nhiêu lần ?

Phương pháp: Dựa vào hình vẽ để tính.

Lời giải chi tiết:

a) Hình được vẽ như sau:

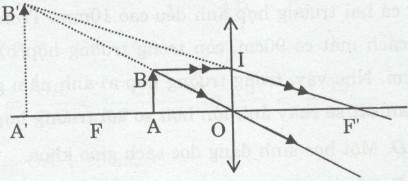
b) Ảnh của vật tạo bởi qua kính lúp là ảnh ảo.

c) Hai tam giác OAB và OA’B’ đồng dạng với nhau nên:

\(\displaystyle{{A'B'} \over {AB}} = {{OA'} \over {OA}} = {{OA'} \over 8}\) (*)

Hai tam giác F’OI và F’A’B’ đồng dạng với nhau nên:

\(\displaystyle{{A'B'} \over {OI}} = {{F'A'} \over {F'O}} = {{10 + OA'} \over {10}} = 1 + {{OA'} \over {10}}\)

Vì OI = AB nên ta có: \(1 + \displaystyle{{OA'} \over {10}} = {{A'B'} \over {AB}} = {{OA'} \over 8}\)  

Suy ra: OA’ = 40cm. Thay vào (*) ta được:

\(\displaystyle{{A'B'} \over {AB}} = {{OA'} \over 8} = {{40} \over 8} = 5\)

Vậy A’B’ = 5AB hay ảnh lớn gấp 5 lần vật

50.6.

a. Dùng kính lúp có tiêu cự 10 cm để quan sát một vật nhỏ cao 1mm. Muốn có ảnh ảo cao 10 mm thì phải đặt vật cách kính bao nhiêu xentimet? Lúc đó ảnh cách kính bao nhiêu xentimet

b. Dùng một thấu kính hội tụ có tiêu cự 40 cm để quan sát vật nói trên. Ta cũng muốn có ảnh ảo cao 10 mm thì phải đặt vật cách kính bao nhiêu xentimet ? Lúc đó ảnh cách kính bao nhiêu xentimet ?

c. Cho rằng trong cả hai trường hợp, người quan sát đều đặt mắt sát sau kính để nhìn ảnh ảo. Hỏi trong trường hợp nào người ấy có cảm giác là ảnh lớn hơn?

Phương pháp: vẽ hình, sử dụng hình vẽ để tính

Lời giải chi tiết:

Hình được vẽ như sau:

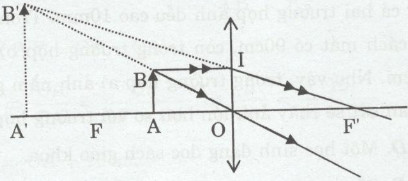
a) Ta có:

\(\eqalign{
& \displaystyle{{A'B'} \over {AB}} = {{F'A'} \over {F'O}} = {{F'O + OA'} \over {F'O}} \cr 
& \Leftrightarrow \displaystyle{{10} \over 1} = {{10 + OA'} \over {10}} \cr 
& \Rightarrow OA' = 90cm \cr} \)

Đồng thời:  

\(\displaystyle{{A'B'} \over {AB}} = {{OA'} \over {OA}} \\\Leftrightarrow \displaystyle{{10} \over 1} = {{90} \over {OA}} \Rightarrow OA = 9cm\)

Vậy vật cách kính 9cm và ảnh cách kính 90cm

b) Tương tự, ta có:

\(\displaystyle{{A'B'} \over {AB}} = {{F'A'} \over {F'O}} = {{F'O + OA'} \over {F'O}} \\\Leftrightarrow \displaystyle{{10} \over 1} = {{40 + OA'} \over {40}}\) 

Suy ra OA’ = 360cm

Đồng thời:

\(\displaystyle{{A'B'} \over {AB}} = {{OA'} \over {OA}} \\\Leftrightarrow \displaystyle{{10} \over 1} = {{360} \over {OA}} \\\Rightarrow OA = 36cm\)

Vậy vật kính 36cm và ảnh cách kính 360cm

c) Trong cả hai trường hợp ảnh đều cao 10mm. Trong trường hợp a) thì ảnh cách mắt có 90cm, còn trong trường hợp b) ảnh cách kính đến 360cm. Như vậy, trong trường hợp a) ảnh nằm gần mắt hơn và người quan sát sẽ thấy ảnh lớn hơn so với trường hợp b).