Bài 50 trang 130 Vở bài tập toán 8 tập 1

Đề bài

Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.

Lời giải chi tiết

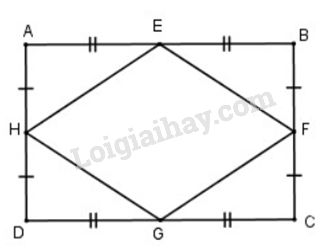
Xét hình chữ nhật \(ABCD\) có \(E,F,G,H\) lần lượt là trung điểm của \(AB,BC,CD,DA\)

Xét  \(∆AEH\) và \(∆BEF\) có:

\(AE = BE \) (vì \(E\) là trung điểm \(AB\))

\(\widehat A = \widehat B = {90^0}\)

\(AH = BF\) (vì \(AH = \dfrac{1}{2}AD \); \(BF= \dfrac{1}{2}BC\); \(AD=BC\) )

Do đó \(∆AEH=∆BEF\) (c.g.c), suy ra \(EH = EF \) (2 cạnh tương ứng)

Chứng minh tương tự ta có: \(EF=GF, GF=GH\).

Tứ giác \(EFGH\) có \(EH = EF= GF=GH\) nên là hình thoi (theo định nghĩa).

Chú ý:

Xét  \(∆HDG\) và \(∆FCG\) có:

\(H{\rm{D}} = FC\left( {cmt} \right)\) (vì \(HD = \dfrac{1}{2}AD \); \(FC= \dfrac{1}{2}BC\); \(AD=BC\) )

\(\widehat D = \widehat C = {90^0}\)

\(DG = CG\) (vì \(G\) là trung điểm \(DC\))

\( \Rightarrow \Delta HDG = \Delta FCG\left( {c - g - c} \right)\)

\( \Rightarrow \) \(GH = GF \) (2 cạnh tương ứng) 

Xét  \(∆AHE\) và \(∆DHG\) có:

\(H{\rm{A}} = HD\) (vì \(H\) là trung điểm \(AD\))

\(\widehat A = \widehat D = {90^0}\)

\(AE = DG\) (vì \(AE = \dfrac{1}{2}AB \); \(DG= \dfrac{1}{2}DC\); \(AB=DC\) )

\(\Rightarrow \Delta AHE = \Delta DHG\left( {c - g - c} \right)\)

\( \Rightarrow \) \(EH = GH \) (2 cạnh tương ứng) 

\( \Rightarrow  HE=EF = GH = GF\).