Bài 48 trang 107 Vở bài tập toán 8 tập 2

Đề bài

Tứ giác \(ABCD\) có \(AB = 4cm, BC = 20 cm\), \(CD = 25 cm, DA = 8cm\), đường chéo \(BD = 10cm\).

a) Nêu cách vẽ tứ giác \(ABCD\) có kích thước đã cho ở trên.

b) Các tam giác \(ABD\) và \(BDC\) có đồng dạng với nhau không? Vì sao?

c) Chứng minh rằng \(AB // CD\).

Lời giải chi tiết

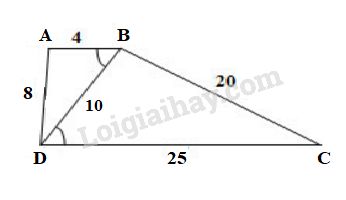
a) Để vẽ được tứ giác \(ABCD\), trước hết ta phải xác định được các đỉnh của nó, sau đó vẽ các cạnh. Cách vẽ như sau:

- Vẽ \(DC = 25\) (h.56), xác định được hai đỉnh \(D,C\) và cạnh \(DC\).

- Lấy \(D\) và \(C\) làm tâm, thứ tự quay hai cung tròn cắt nhau có bán kính là \(10cm\) và \(20cm\), xác định được đỉnh \(B\).

- Lấy \(B\) và \(D\) làm tâm, thứ tự quay hai cung tròn cắt nhau có bán kính là \(4cm\) và \(8cm\), xác định được đỉnh \(A\).

- Vẽ các đoạn thẳng \(CB,DB,DA,AB\) được tứ giác \(ABCD\) thỏa mãn các yêu cầu của bài toán.

b) Xét hai tam giác \(ABD\) và \(BDC\), ta thấy:

\(\dfrac{{AB}}{{BD}} = \dfrac{4}{{10}} = \dfrac{2}{5}\); \(\dfrac{{AD}}{{BC}} = \dfrac{8}{{20}} = \dfrac{2}{5};\) \(\dfrac{{BD}}{{DC}} = \dfrac{{10}}{{25}} = \dfrac{2}{5}\)

Do đó \(\dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} = \dfrac{{BD}}{{DC}}\) \( \Rightarrow \Delta ABD \backsim \Delta BDC\) (c.c.c)

c) Hai tam giác \(ABD\) và \(BDC\) đồng dạng với nhau do đó các góc tương ứng phải bằng nhau.

\(\Delta ABD \backsim \Delta BDC\) \( \Rightarrow \widehat {ABD} = \widehat {BDC}\) \( \Rightarrow AB//CD\) (hai góc so le trong bằng nhau).