Bài 46 trang 163 SBT toán 8 tập 1

Đề bài

Hai đường chéo của một hình thoi có độ dài là \(16\,cm\) và \(12\,cm.\) Tính:

a) Diện tích hình thoi

b) Độ dài cạnh hình thoi

c) Độ dài đường cao hình thoi

Lời giải chi tiết

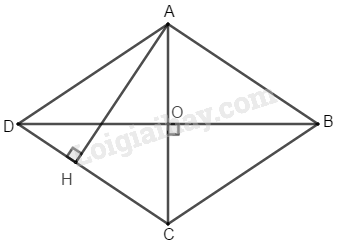
Giả sử ABCD là hình thoi có \(AC=12cm, BD=16cm\) và O là giao điểm hai đường chéo

Suy ra \(AC \bot BD\) và \(O\) là trung điểm của AC, BD.

Do đó \(OA = \dfrac{{AC}}{2};OB = \dfrac{{BD}}{2}\)

a. \(S_{ABCD} = AC.BD = \dfrac{1}{2}.12.16 = 96\) \((cm^2)\)

b.Trong tam giác vuông \(OAB\), theo định lý Pytago ta có:

\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} \\= {\left( {\dfrac{{AC}}{2}} \right)^2} + {\left( {\dfrac{{BD}}{2}} \right)^2} \\= {6^2} + {8^2} = 100\\ \Rightarrow AB = 10(cm)\end{array}\)

Vậy cạnh hình thoi là \(10cm\).

c. Kẻ \(AH ⊥ CD\) (\(H ∈ CD\))

\(\eqalign{  & {S_{ABCD}} = AH.CD  \cr  &  \Rightarrow AH = {{{S_{ABCD}}} \over {CD}} = {{96} \over {10}} = 9,6(cm) \cr} \)