Bài 4.46 trang 116 SBT đại số 10

Biểu diễn hình học tập nghiệm của các bất phương trình sau:

LG a

\(3 + 2y > 0;\)

Phương pháp giải:

Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng \((\Delta )\): \(ax + by = c\)

Bước 2: Lấy một điểm \({M_0}({x_0},{y_0}) \notin \Delta \), thường lấy gốc tọa độ

Bước 3: Tính \(a{x_0} + b{y_0}\) và so sánh \(a{x_0} + b{y_0}\) với c

Bước 4: Kết luận

Lời giải chi tiết:

Vẽ đường thẳng 3+2y=0 hay \(y =  - \dfrac{3}{2}\) trên mặt phẳng tọa độ:

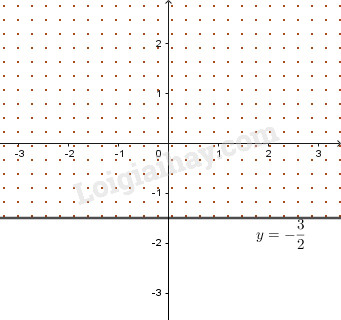
Điểm \(O(0,0)\) có tọa độ thỏa mãn bất phương trình, do đó miền nghiệm là nửa mặt phẳng bờ \(3 + 2y = 0\) chứa \(O\) (phần dấu chấm trên hình, bỏ bờ).

LG b

\(2x - 1 < 0;\)

Lời giải chi tiết:

Vẽ đường thẳng \(2x-1=0\) hay \(x = \dfrac{1}{2}\) trên mặt phẳng Oxy.

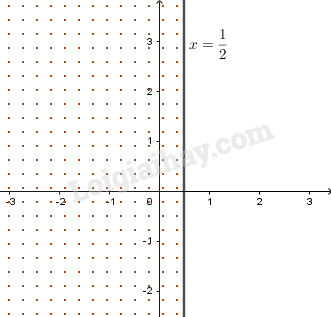
Miền nghiệm là nửa mặt phẳng bờ \(2x - 1 = 0\) chứa \(O\) (phần dấu chấm trên hình, bỏ bờ).

LG c

\(x - 5y < 2;\)

Lời giải chi tiết:

Vẽ đường thẳng \(  x - 5y =   2\) trên mặt phẳng tọa độ.

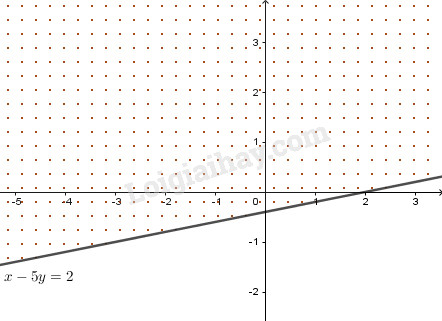
Miền nghiệm là nửa mặt phẳng bờ \(x + 5y =  2\) chứa \(O\) (phần dấu chấm trên hình, bỏ bờ).

LG d

\(2x + y > 1\)

Lời giải chi tiết:

Vẽ đường thẳng \(2x+y=1\) trên mặt phẳng tọa độ.

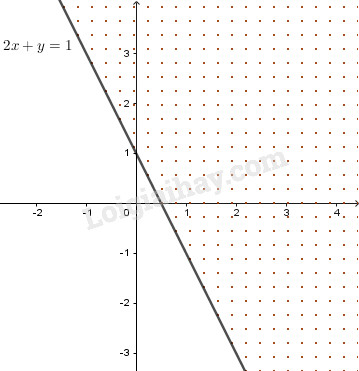
Miền nghiệm là nửa mặt phẳng bờ \(2x + y = 1\) không chứa \(O\) (phần dấu chấm trên hình, bỏ bờ).

LG e

 \( - 3x + y + 2 \le 0\)

Lời giải chi tiết:

Vẽ đường thẳng \(-3x+y=-2\) trên mặt phẳng tọa độ.

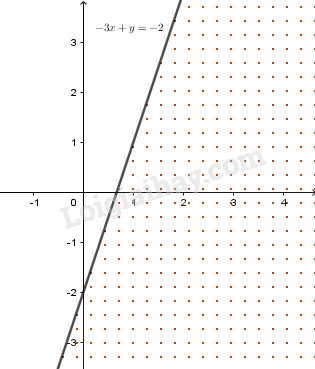
Miền nghiệm là nửa mặt phẳng bờ \( - 3x + y =  - 2\) không chứa \(O\) (phần dấu chấm trên hình).

LG f

\(2x - 3y + 5 \ge 0.\)

Lời giải chi tiết:

Vẽ đường thẳng \(2x-3y=-5\) trên mặt phẳng tọa độ.

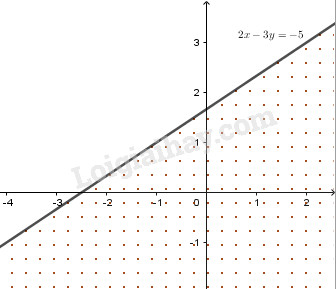
Miền nghiệm là nửa mặt phẳng bờ \(2x - 3y =  - 5\) chứa điểm O (phần dấu chấm trên hình).