Bài 4.2 phần bài tập bổ sung trang 85 SBT toán 8 tập 1
Giải bài 4.2 phần bài tập bổ sung trang 85 sách bài tập toán 8. Cho đường thẳng d và hai điểm A, B có khoảng cách đến đường thẳng d theo thứ tự là 20cm và 6cm. Gọi C là trung điểm của AB. Tính khoảng cách từ C đến đường thẳng d.
Đề bài
Cho đường thẳng \(d\) và hai điểm \(A, B\) có khoảng cách đến đường thẳng \(d\) theo thứ tự là \(20cm\) và \(6cm.\) Gọi \(C\) là trung điểm của \(AB.\) Tính khoảng cách từ \(C\) đến đường thẳng \(d.\)
Phương pháp giải - Xem chi tiết
* Chú ý: Chia hai trường hợp: \(A, B\) cùng phía với \(d\) và \(A,B\) khác phía với \(d.\)
Sử dụng định nghĩa, tính chất đường trung bình của tam giác và hình thang:
+) Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
+) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
+) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
\(a)\) Trường hợp \(A\) và \(B\) nằm trên một nửa mặt phẳng bờ chứa đường thẳng \(d.\)
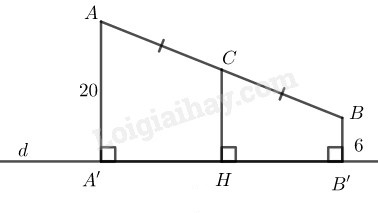
Gọi \(A’, B’\) là chân đường vuông góc kẻ từ \(A\) và \(B\) đến \(d\)
\(AA’ ⊥ d;\) \(BB’ ⊥ d \)\(⇒ AA’ // BB’\)
Tứ giác \(ABB’A’\) là hình thang. Kẻ \(CH ⊥ d\)
\(⇒ CH // AA’ // BB’\) nên \(CG\) là đường trung bình của hình thang \(ABB’A’\)
\( \Rightarrow CH = \displaystyle {{AA' + BB'} \over 2}\)\( = \displaystyle {{20 + 6} \over 2} = 13\,\,\left( {cm} \right)\)
\(b)\) Trường hợp \(A\) và \(B\) nằm trên hai nửa mặt phẳng đối bờ chứa đường thẳng \(d\)
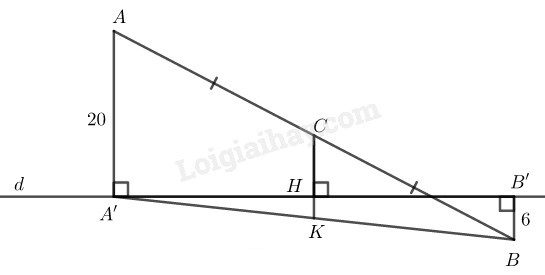
Kẻ \(CH ⊥ d\) cắt \(A’B\) tại \(K\)
\(⇒ CH // AA’ // BB’\)
Trong \(∆ AA’B\) ta có: \(AC = CB\)
Mà \(CK // AA’\) nên \(A’K = KB\) và \(CK\) là đường trung bình của tam giác \(AA’B\)
\( \Rightarrow CK =\displaystyle {{AA'} \over 2}\) (tính chất đường trung bình của tam giác)
\(CK = \displaystyle {{20} \over 2} = 10\,\,\left( {cm} \right)\)
Trong \(∆ A’BB’\) có \(A’K = KB\) và \(KH // BB’\)
Nên \(KH\) là đường trung bình của \(∆ A’BB’\)
\( \Rightarrow KH =\displaystyle {{BB'} \over 2}\) (tính chất đường trung bình của tam giác)
\( \Rightarrow KH = \displaystyle {6 \over 2} = 3\,\,\left( {cm} \right)\)
\(CH = CK – KH = 10 – 3 = 7\;\;(cm)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4.2 phần bài tập bổ sung trang 85 SBT toán 8 tập 1 timdapan.com"







