Bài 38 trang 84 SBT toán 8 tập 1
Giải bài 38 trang 84 sách bài tập toán 8. Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE // IK, DE = IK.
Đề bài
Cho tam giác \(ABC,\) các đường trung tuyến \(BD\) và \(CE\) cắt nhau ở \(G.\) Gọi \(I, K\) theo thứ tự là trung điểm của \(GB, GC.\) Chứng minh rằng \(DE // IK,\) \(DE = IK.\)
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa, tính chất đường trung bình của tam giác:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
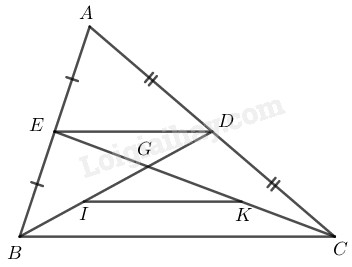
Trong tam giác \(ABC\) ta có:
\(E\) là trung điểm của \(AB \;\;(gt)\)
\(D\) là trung điểm của \(AC\;\; (gt)\)
Nên \(ED\) là đường trung bình của tam giác \(ABC\)
\(⇒ED // BC\) và \(ED = \displaystyle{{BC} \over 2}\) (tính chất đường trung bình của tam giác) \((1)\)
Trong tam giác \(GBC\) ta có:
\(I\) là trung điểm của \(BG\;\; (gt)\)
\(K\) là trung điểm của \(CG\;\; (gt)\)
Nên \(IK\) là đường trung bình của \(∆ GBC\)
\(⇒ IK // BC\) và \(IK = \displaystyle {{BC} \over 2}\) (tính chất đường trung bình của tam giác) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(IK // DE\) và \(IK = DE.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 38 trang 84 SBT toán 8 tập 1 timdapan.com"







