Bài 40 trang 162 SBT toán 8 tập 1

Đề bài

Hai cạnh của một hình bình hành có độ dài là \(6\,cm\) và \(8\,cm.\) Một trong các đường cao có độ dài là \(5\,cm.\) Tính độ dài đường cao thứ hai. Hỏi bài toán có mấy đáp số ?

Lời giải chi tiết

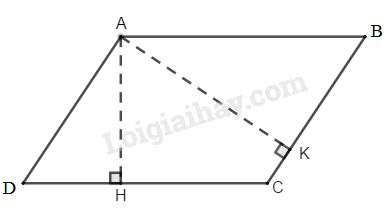
Giả sử hình bình hành \(ABCD\) có \(AB = 8cm,\, AD = 6cm.\)

Kẻ \(AH ⊥ CD,\, AK ⊥ BC\) 

Ta có \(5 cm< 6 cm;\, 5cm < 8cm\)

Đường cao là cạnh góc vuông nhỏ hơn cạnh huyền thỏa mãn có hai trường hợp:

+) Nếu \(AK = 5cm,\) khi đó

\(\begin{array}{l}{S_{ABCD}} = AK.BC = 5.6 = 30(c{m^2})\\{S_{ABCD}} = AH.AD = 8.AH\\ \Rightarrow 8.AH = 30 \\\Rightarrow AH =\dfrac{{30}}{8} = \dfrac{{15}}{4}(cm)\end{array}\)

+) Nếu \(AH = 5cm\)

\(\begin{array}{l}{S_{ABCD}} = AH.CD = 5.8 = 40(c{m^2})\\{S_{ABCD}} = AK.BC = 6.AK\\ \Rightarrow 6.AK = 40 \\\Rightarrow AK = \dfrac{{40}}{6} = \dfrac{{20}}{3}(cm)\end{array}\)

Vậy đường cao thứ hai có độ dài là \(\dfrac{{15}}{4}(cm)\) cm hoặc \(\dfrac{{20}}{3}\) \((cm)\)