Giải Bài 4 trang 58 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC có góc A là góc từ. Các đường trung trực của AB và Ac cắt nhau tại O và lần lượt cắt BC tại E và F. Hãy chứng minh
Đề bài
Cho tam giác ABC có góc A là góc từ. Các đường trung trực của AB và Ac cắt nhau tại O và lần lượt cắt BC tại E và F. Hãy chứng minh
a) \(\Delta EO{\rm{A}} = \Delta EOB,\Delta F{\rm{O}}A = \Delta F{\rm{O}}C\)
b) Chứng minh rằng AO là tia phân giác của góc EAF.
Phương pháp giải - Xem chi tiết
- Tìm các điều kiện để hai tam giác bằng nhau.
- Chứng minh: \(\widehat {OA{\rm{E}}} = \widehat {OAF}\) suy ra AO là tia phân giác của góc EAF
Lời giải chi tiết
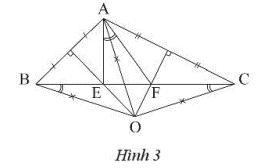
a) E và O nằn trên đường trung trực của AB nên ta có EA = EB, OA = OB.
F và O nằm trên đường trung trực của AC nên ta có FA = FC, OA = OC
Suy ra: \(\Delta EO{\rm{A}} = \Delta EOB\)(c – c – c) vì EO chung, EA = EB, OA = OB
\(\Delta F{\rm{O}}A = \Delta F{\rm{O}}C(c - c - c)\) vì FO chung, FA = FC, OA = OC.
b) Ta có OA = OC và OA = OB nên OB = OC suy ra tam giác OBC cân tại O suy ra \(\widehat {OBE} = \widehat {OCF}(1)\)
Ta có \(\Delta EO{\rm{A}} = \Delta EOB\); \(\Delta F{\rm{O}}A = \Delta F{\rm{O}}C\) do đó: \(\widehat {OA{\rm{E}}} = \widehat {OBE};\widehat {OAF} = \widehat {OCF}(2)\)
Từ (1) và (2) ta có: \(\widehat {OA{\rm{E}}} = \widehat {OAF}\) suy ra AO là tia phân giác của góc EAF.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Bài 4 trang 58 sách bài tập toán 7 - Chân trời sáng tạo timdapan.com"







