Giải bài 39 trang 82, 83 sách bài tập toán 11 - Cánh diều

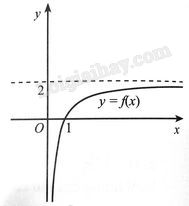
Quan sát đồ thị hàm số trong hình dưới đây và cho biết:

LG a

\(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right)\) bằng:

A. \(2\)                                    

B. \(1\)                          

C. \( + \infty \)              

D. \( - \infty \)

Phương pháp giải:

Sử dụng đồ thị hàm số để xác định các giới hạn, và tính liên tục của hàm số đó.

Lời giải chi tiết:

 Từ đồ thị, ta nhận xét rằng khi \(x \to  + \infty \) thì \(f\left( x \right)\) tiến dần tới 2. Do vậy \(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = 2\). Đáp án đúng là A.

LG b

\(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right)\) bằng:

A. \(2\)                                    

B. \(1\)                          

C. \( + \infty \)              

D. \( - \infty \)

Phương pháp giải:

Sử dụng đồ thị hàm số để xác định các giới hạn, và tính liên tục của hàm số đó.

Lời giải chi tiết:

Từ đồ thị, ta nhận xét rằng khi \(x\) tiến tới 0 về bên phải thì \(f\left( x \right)\) tiến dần tới âm vô cực. Do vậy \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) =  - \infty \). Đáp án đúng là D.

LG c

Hàm số \(y = f\left( x \right)\) liên tục trên khoảng:

A. \(\left( { - \infty ;1} \right)\)                            

B. \(\left( { - \infty ; + \infty } \right)\)      

C. \(\left( {1; + \infty } \right)\)            

D. \(\left( { - \infty ;2} \right)\)

Phương pháp giải:

Sử dụng đồ thị hàm số để xác định các giới hạn, và tính liên tục của hàm số đó.

Lời giải chi tiết:

Nhận xét rằng hàm số chỉ nằm ở bên phải trục tung, nên tập xác định của chúng là \(\left( {0, + \infty } \right)\). Suy ra các đáp án A, B, D sai.

Nhận xét rằng trên khoảng \(\left( {1, + \infty } \right)\), đồ thị hàm số là “đường liền”, nên hàm số liên tục trên khoảng \(\left( {1, + \infty } \right)\).

Đáp án đúng là C.