Bài 39 trang 25 SBT toán 7 tập 2
Giải bài 39 trang 25 sách bài tập toán 7. Tính f(x) – g(x) với:...
Đề bài
Tính \(f(x) – g(x)\) với:
\(f(x) = {x^7} - 3{{\rm{x}}^2} - {x^5} + {x^4}\)\( - {x^2} + 2{\rm{x}} - 7\)
\(g(x) = x - 2{{\rm{x}}^2} + {x^4} - {x^5}\)\( - {x^7} - 4{{\rm{x}}^2} - 1\)
Phương pháp giải - Xem chi tiết
Bước 1: Nhóm các hạng tử đồng dạng với nhau để thu gọn các đa thức
Bước 2: Đặt phép tính theo hàng ngang hoặc hàng dọc rồi thực hiện phép cộng (trừ) các đa thức.
Lời giải chi tiết
Thu gọn và sắp xếp các đa thức, ta được:
\( +)\,f(x) = {x^7} - 3{{\rm{x}}^2} - {x^5} + {x^4} - {x^2}\)\( + 2{\rm{x}} - 7\)
\(= {x^7} +(- 3{{\rm{x}}^2}-x^2) - {x^5} + {x^4} \)\( + 2{\rm{x}} - 7\)
\(= {x^7} +(- 3-1){{\rm{x}}^2} - {x^5} + {x^4} \)\( + 2{\rm{x}} - 7\)
\(= {x^7} -4{{\rm{x}}^2} - {x^5} + {x^4} \)\( + 2{\rm{x}} - 7\)
\( = {x^7} - {x^5} + {x^4} - 4{x^2} + 2{\rm{x}} - 7 \)
\(+)\, g(x) = x - 2{{\rm{x}}^2} + {x^4} - {x^5} - {x^7}\)\( - 4{{\rm{x}}^2} - 1 \)
\(=- {x^7} - {x^5} + {x^4} \)\(+(- 2{{\rm{x}}^2}-4x^2) + x - 1\)
\(=- {x^7} - {x^5} + {x^4} \)\(+(- 2-4){{\rm{x}}^2} + x - 1\)
\( = - {x^7} - {x^5} + {x^4} - 6{{\rm{x}}^2} + x - 1 \)
Suy ra:
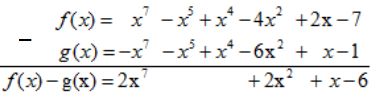
Hay \(f(x)-g(x)=2x^7+2x^2+x-6\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 39 trang 25 SBT toán 7 tập 2 timdapan.com"







