Bài 38 trang 25 SBT toán 7 tập 2
Giải bài 38 trang 25 sách bài tập toán 7. Tính f(x) + g(x) với:...
Đề bài
Tính \(f(x) + g(x)\) với:
\(f\left( x \right) = {x^5} - 3{{\rm{x}}^2} + {x^3} - {x^2} - 2{\rm{x}} + 5\)
\(g\left( x \right) = {x^2} - 3{\rm{x}} + 1 + {x^2} - {x^4} + {x^5}\)
Phương pháp giải - Xem chi tiết
Bước 1: Nhóm các hạng tử đồng dạng với nhau để thu gọn các đa thức
Bước 2: Đặt phép tính theo hàng ngang hoặc hàng dọc rồi thực hiện phép cộng (trừ) các đa thức.
Lời giải chi tiết
Thu gọn các đa thức:
\(\eqalign{
& f\left( x \right) = {x^5} - 3{{\rm{x}}^2} + {x^3} - {x^2} - 2{\rm{x}} + 5 \cr
&=x^5+(-3x^2-x^2)+x^3-2x+5\cr &=x^5+(-3-1)x^2+x^3-2x+5\cr&=x^5-4x^2+x^3-2x+5\cr
&= {x^5} + {x^3} - 4{x^2} - 2{\rm{x}} + 5 \cr} \)
\(\eqalign{
& g\left( x \right) = {x^2} - 3{\rm{x}} + 1 + {x^2} - {x^4} + {x^5}\cr
&= x^5-x^4+(x^2+x^2)-3x+1\cr &= x^5-x^4+(1+1)x^2-3x+1\cr
& = {x^5} - {x^4} + 2{x^2} - 3{\rm{x}} + 1 \cr} \)
Suy ra:
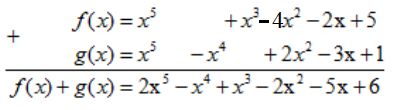
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 38 trang 25 SBT toán 7 tập 2 timdapan.com"







