Bài 37 trang 140 Vở bài tập toán 9 tập 1

Đề bài

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, \(B \in \left( O \right),C \in \left( {O'} \right)\). Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O’M và AC. Chứng minh rằng:

a) Tứ giác AEMF là hình chữ nhật

b) ME.MO = MF.MO’

c) OO’ là tiếp tuyến của đường tròn có đường kính là BC 

d) BC là tiếp tuyến của đường tròn có đường kính là OO’

Lời giải chi tiết

a)

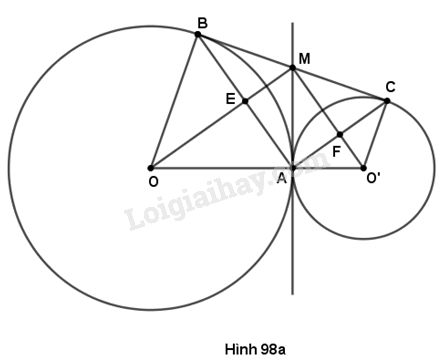
(h. 98a) Theo tính chất hai tiếp tuyến cắt nhau của đường tròn \(\left( O \right),\) ta có \(MA = MB,\) \(MO\) là tia phân giác của \(\widehat {BMA}.\)

Tam giác \(AMB\) cân tại \(M,\) có \(MO\) là tia phân giác nên \(MO \bot AB.\)

Chứng minh tương tự với đường tròn \(\left( {O'} \right),\) ta có \(MA = MC,MO'\) là tia phân giác của \(\widehat {AMC}\) nên \(MO' \bot AC.\)

Do \(MO\) và \(MO'\) là hai tia phân giác của hai góc kề bù nên \(\widehat {OMO'} = {90^o}.\)

Tứ giác \(AEMF\) có ba góc vuông nên là hình chữ nhật.

b) Tam giác \(MAO\) vuông tại \(A,\)đường cao \(AE\) nên \(ME.MO = M{A^2}{\rm{                (1)}}\)

Tam giác   \(MAO'\) vuông tại \(A,\)đường cao \(AF\) nên \(MF.MO' = M{A^2}{\rm{                (2)}}\)

Từ (1) và (2) suy ra \(ME.MO = MF.MO'.\)

c) Đường tròn đường kính \(BC\) có tâm \(M,\) bán kính \(MA.\) Ta có \(OO' \bot MA\) (vì \(MA\) là tiếp tuyến của đường tròn \((O)\) và \(\left( {O'} \right)\)).

Đường thẳng \(OO'\) vuông góc với bán kính \(MA\) của đường tròn \(\left( M \right)\) tại \(A\) nên \(OO'\) là tiếp tuyến của đường tròn \(\left( M \right),\) tức là tiếp tuyến của đường tròn có đường kính là \(BC.\)

d)

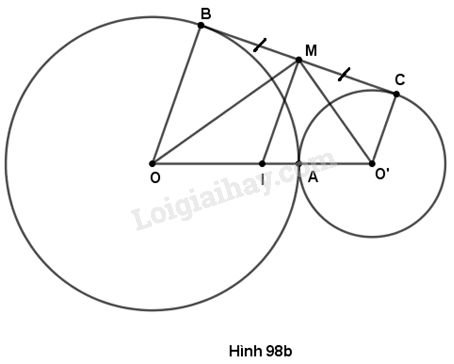
(h. 98b) Gọi I là trung điểm của \(OO'.\)

Đường tròn đường kính \(OO'\) có tâm là \(I,\) bán kính là \(IM\) (vì \(MI\) là đường trung tuyến ứng với cạnh huyền của tam giác vuông \(OMO'\) nên \(MI = IO = IO'\))

Hình thang \(OBCO'\left( {OB//O'C} \right)\) có \(BM = MC;OI = O'I\) nên \(IM\) là đường trung bình, suy ra \(IM//OB//O'C.\)

Ta lại có \(OB \bot BC\) nên \(IM \bot BC.\)

Đường thẳng \(BC\) vuông góc với bán kính \(IM\) của đường tròn \(\left( I \right)\) tại \(M\) nên \(BC\) là tiếp tuyến của đường tròn \(\left( I \right),\) tức là tiếp tuyến của đường tròn có đường kính \(OO'.\)