Bài 36 trang 138 Vở bài tập toán 9 tập 1

Đề bài

Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H. Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.

a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).

b) Tứ giác AEHF là hình gì ? vì sao ?

c) Chứng minh đẳng thức AE.AB = AF.AC 

d) Dây AD vuông góc với BC tại vị trí nào thì EF có độ dài lớn nhất ?

Lời giải chi tiết

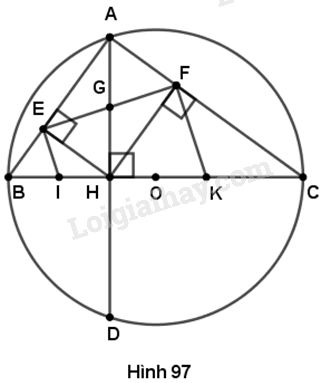
a) Đường tròn \(\left( I \right)\) có bán kính là \(BI.\)

Đường tròn \(\left( O \right)\) có bán kính là \(OB.\)

Ta có \(OI = OB - BI\) nên hai đường tròn tiếp xúc trong.

- Đường tròn \(\left( K \right)\) có bán kính là \(KC.\)

Đường tròn \(\left( O \right)\) có bán kính là \(OC.\)

Ta có \(OK = OC - KC\) nên hai đường tròn tiếp xúc trong.

- Đường tròn \(\left( I \right)\) có bán kính là \(IH.\)

Đường tròn \(\left( K \right)\) có bán kính là \(HK.\)

Ta có \(IK = IH + HK\) nên hai đường tròn tiếp xúc ngoài.

b) \(\widehat {BAC} = {90^o}\) vì tam giác \(ABC\) nội tiếp đường tròn đường kính \(AB.\)

\(\widehat {AEH} = {90^o}\) vì \(HE \bot AB,\widehat {AFH} = {90^o}\)vì \(HE \bot AC.\)

Tứ giác \(AEHF\) có ba góc vuông nên là hình chữ nhật.

c) Tam giác \(AHB\) vuông tại \(H,\) đường cao \(AH\) nên \(AE.AB = A{H^2}{\rm{      }}\left( 1 \right)\)

Tam giác \(AHC\) vuông tại  \(H,\) đường cao \(AH\) nên \(AF.AC = A{H^2}{\rm{      }}\left( 2 \right)\)

Từ (1) và (2) suy ra \(AE.AB = AF.AC\)

d) Ta cần chứng minh \(KF \bot EF\) và \(IE \bot EF.\)

Gọi \(G\) là giao điểm của \(AH\) và \(EF,\) ta có \(AEHF\) là hình chữ nhật (theo câu b), do đó \(GH = GA;GF = GE,\) mà \(AH = EF\) nên \(GH = GF,\) suy ra \(\widehat {GFH} = \widehat {GHF}{\rm{                  }}\left( 3 \right)\)

Tam giác \(KHF\) cân tại \(K\) nên \(\widehat {KFH} = \widehat {KHF}{\rm{                  (4)}}\)

Từ (3) và (4) suy ra  \(\widehat {GFH} + \widehat {KFH} = \widehat {GHF} + \widehat {KHF},\) tức là \(\widehat {GFK} = \widehat {AHK}.\)

Ta lại có \(\widehat {AHK} = {90^o}\) nên \(\widehat {GFK} = {90^o}.\)

Đường thẳng \(EF\) vuông góc với bán kính \(FK\) tại \(F\) nên \(EF\) là tiếp tuyến của \(\left( K \right).\)

Chứng minh tương tự, \(EF\) là tiếp tuyến của \(\left( I \right).\)

Vậy \(EF\) là tiếp tuyến chung của hai đường tròn \(\left( I \right)\) và \(\left( K \right).\)

e) Theo tính chất hình chữ nhật, \(EF = AH.\)

Đường kính \(BC\) vuông góc với dây \(AD\) nên \(AH = HD = \dfrac{1}{2}AD.\)

Suy ra \(EF = \dfrac{1}{2}AD.\)

Do đó \(EF\) lớn nhất \( \Leftrightarrow AD\) lớn nhất. Ta có \(AD\) là dây của đường tròn \(\left( O \right),\) do đó \(AD\) lớn nhất khi \(AD\) là đường kính , khi đó điểm \(H\) trùng với điểm \(O.\)

Vậy khi dây \(AD\) vuông góc với \(BC\) tại điểm \(O\) thì \(EF\) có độ dài lớn nhất.