Bài 36.10, 36.11, 36.12, 36.13 trang 88,89 SBT Vật lí 10

36.10.

Một thanh thép ở \({20^0}C\)có tiết diện \(4c{m^2}\)và hai đầu của nó được gắn chặt vào hai bức tường đối diện. Xác định lực do thanh thép tác dụng lên hai bức tường nếu nó bị nung nóng đến \({200^0}C\) ? Cho biết suất đàn hồi của thép \({21,6.10^{10}}Pa\)và hệ số nở dài của nó là \({11.10^{ - 6}}{K^{ - 1}}\)

Phương pháp giải:

Áp dụng công thức \(\sigma  = \dfrac{F}{S} = E\dfrac{{\left| {\Delta \ell } \right|}}{{{\ell _0}}}\)

Lời giải chi tiết:

Một thanh thép ở \({20^0}C\)có tiết diện \(4c{m^2}\)và hai đầu của nó được gắn chặt vào hai bức tường đối diện. Xác định lực do thanh thép tác dụng lên hai bức tường nếu nó bị nung nóng đến \({200^0}C\) ? Cho biết suất đàn hồi của thép \({21,6.10^{10}}Pa\)và hệ số nở dài của nó là \({11.10^{ - 6}}{K^{ - 1}}\)

- Thanh thép khi bị nung nóng từ nhiệt độ\({t_1}\) đến \({t_2}\) : \(\dfrac{{\Delta \ell }}{\ell } = \alpha ({t_2} - {t_1})\)

 - Thanh thép khi bị biến dạng kéo tính theo định luật Húc : \(\dfrac{{\Delta \ell }}{\ell } = \dfrac{1}{E}FS\)So sánh hai công \({t_1} = {20^0}C\)đến \({t_2} = {20^0}C\)tính bằng : \(F = {\rm{ES}}\alpha {\rm{(}}{{\rm{t}}_2} - {t_1}) = {21,6.10^{10}}{.4.10^{ - 4}}{.11.10^{ - 6}}(200 - 20)\~171kN\)F = ESα(t₂ – t₁) = 21,6.10¹⁰.4.10^-4.11.10^-6.(200 – 20) ≈ 171 kN.

36.11.

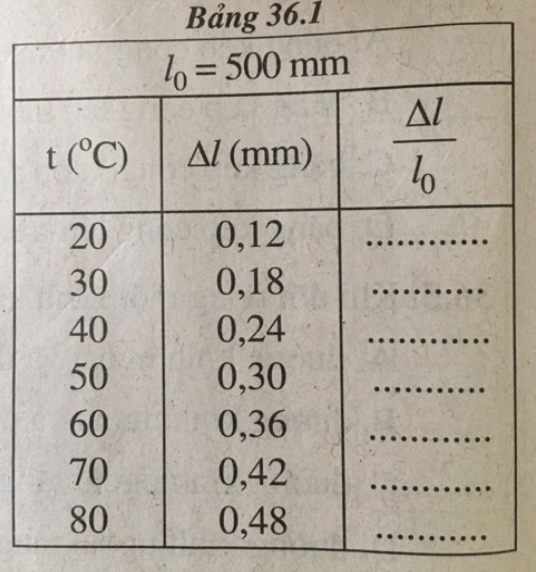
Khi tiến hành thí nghiệm khảo sát sự nở dài vì nhiệt của vật rắn, các kết quả đo độ dài \({\ell _0}\) của thanh thép  ở và độ nở dài \(\Delta \ell \)của nó ứng với độ tăng nhiệt độ t (tính từ \({0^0}C\) đến \({t^0}C\)) được ghi trong Bảng 36.1 :

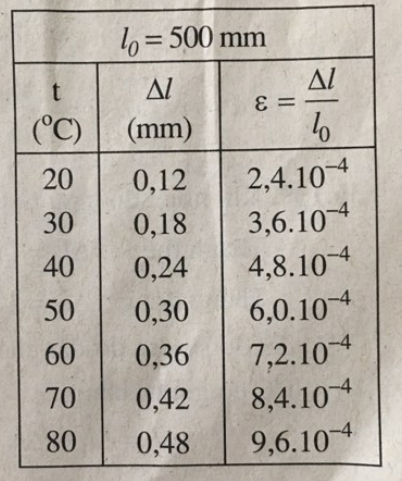
a) Tính độ dãn dài tỉ đối \(\dfrac{{\Delta \ell }}{{{\ell _0}}}\) của thanh thép ở những nhiệt độ t khác nhau được ghi trong Bảng 36.1.

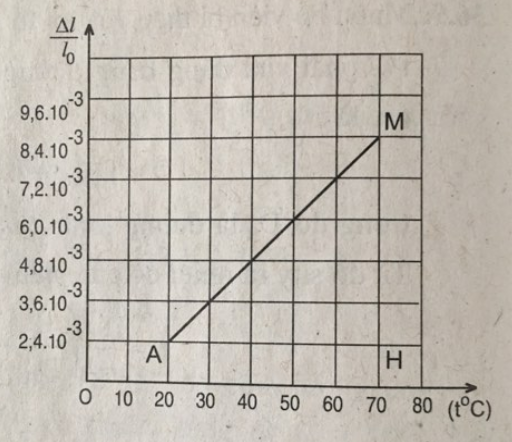
b) Vẽ đồ thị biểu diễn sự phụ thuộc của độ dãn dài tỉ đối \(\dfrac{{\Delta \ell }}{{{\ell _0}}}\) vào nhiệt độ t của thanh thép.

c) Dựa vào đồ thị vẽ được, tính giá trị trung bình của hệ số nở dài α của thanh thép.

Phương pháp giải:

Áp dụng công thức \(\Delta \ell  = {\ell _0}.\alpha \Delta t\)

Lời giải chi tiết:

a) Kết quả tính độ dãn dài tỉ đối của thanh thép ở những nhiệt độ t khác nhau (được ghi ở bảng bên)

b) Chọn tỉ xích trên các trục toạ độ :

Trục hoành : \(1cm \to t = {10^0}C\)

Trục tung : \(1cm \to \dfrac{{\Delta \ell }}{{{\ell _0}}} = {1,2.10^{ - 4}}\)

Đường biểu diễn đồ thị vẽ được trên hình vẽ trên có dạng đoạn thẳng.

Điều này chứng tỏ độ biến dạng tỉ đối \(\dfrac{{\Delta \ell }}{{{\ell _0}}}\) của thanh sắt tỉ lệ thuận với độ tăng nhiệt độ t (tính từ\({0^0}C\)): \(\dfrac{{\Delta \ell }}{{{\ell _0}}} = \alpha t\)

Nhận xét thấy hệ số tỉ lệ \(\alpha \) chính là hệ số nở dài của thép.

Hệ số tỉ lệ \(\alpha \) được xác định bởi hệ số góc của đường biểu diễn đồ thị ở hình vẽ

36.12.

Một tấm đồng hình vuông ở \({0^0}C\) có cạnh dài 50 cm. Khi bị nung nóng tới nhiệt độ \({t^0}C\), diện tích của đồng tăng thêm \(17c{m^2}\). Tính nhiệt độ nung nóng \({t^0}C\) của tấm đồng. Hệ số nở dài của đồng là \({17.10^{ - 6}}{K^{ - 1}}\).

Phương pháp giải:

 Áp dụng công thức \(\Delta \ell  = {\ell _0}.\alpha \Delta t\)

Lời giải chi tiết:

Diện tích tấm đồng hình vuông ở \({0^0}C\) là \({S_0} = \ell _0^2\). Khi bị nung nóng, kích thước của tấm đồng tăng theo mọi hướng, nên diện tích của tấm đồng này ở \({t^0}C\) sẽ là :

\(S = {\ell ^2} = {({\ell _0} + \Delta \ell )^2} = \ell _0^2 + 2{\ell _0}\Delta \ell  + {(\Delta \ell )^2}\)

Theo công thức nở dài : \(\Delta \ell  = \Delta {\ell _0}\Delta t\)

Vì \(\alpha  = {17.10^{ - 6}}{K^{ - 1}}\) khá nhỏ và \(\Delta t = t - {t_0} = t\) không lớn, nên \(\Delta \ell  <  < {\ell _0}\)

Do đó, bỏ qua \(\Delta {\ell ^2}\)và coi gần đúng.:

\(S\approx {S_0} + 2{\ell _0}\Delta \ell \) hay \(\Delta S = S - {S_0} = 2\alpha {S_0}\Delta t\)

Từ đó suy ra : \(t\approx \dfrac{{\Delta S}}{{2\alpha {S_0}}} = \dfrac{{{{17.10}^{ - 4}}}}{{{{2.17.10}^{ - 6}}.{{(0,5)}^2}}} = {200^0}C\)

36.13.

Xác định độ dài của thanh thép và của thanh đồng ở \({0^0}C\) sao cho ở bất kì nhiệt độ nào thanh thép luôn dài hơn thanh đồng một đoạn bằng 50 mm. Cho biết hệ số nở dài của đồng là \({16.10^{ - 6}}{K^{ - 1}}\) và của thép là \({12.10^{ - 6}}{K^{ - 1}}\)

Phương pháp giải:

 Áp dụng công thức \(\Delta \ell  = {\ell _0}.\alpha \Delta t\)

Lời giải chi tiết:

Khi nhiệt độ tăng từ \({0^0}C\) đến \({t^0}C\)thì độ dãn dài của :

- Thanh thép : \(\Delta {\ell _1} = {\ell _{01}}{\alpha _1}t\)

 - Thanh đồng : \(\Delta {\ell _2} = {\ell _{02}}{\alpha _2}t\)

Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t^oC có giá trị bằng :

\(\Delta \ell  = \Delta {\ell _1} - \Delta {\ell _2} \\= {\ell _{01}}{\alpha _1}t - {\ell _{02}}{\alpha _2}t \\= ({\ell _{01}}{\alpha _1} - {\ell _{02}}{\alpha _2})t = 50mm\)

Công thức này chứng tỏ \(\Delta \ell \) phụ thuộc bậc nhất vào t. Rõ ràng, muốn \(\Delta \ell \) không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :

\({\ell _{01}}{\alpha _1} - {\ell _{02}}{\alpha _2} = 0 \\\to \dfrac{{{\ell _{02}}}}{{{\ell _{01}}}} = \dfrac{{{\alpha _1}}}{{{\alpha _2}}}\)

hay:

\(\dfrac{{{\ell _{02}}}}{{{\ell _{01}} - {\ell _{02}}}} = \dfrac{{{\alpha _1}}}{{{\alpha _2} - {\alpha _1}}} = \dfrac{{{{12.10}^{ - 6}}}}{{{{16.10}^{ - 6}} - {{12.10}^{ - 6}}}} = 3\)

Từ đó suy ra độ dài ở \({0^0}C\) của :

- Thanh đồng : \({\ell _{02}} = 3({\ell _{01}} - {\ell _{02}}) = \Delta \ell  = 3.50 = 150mm\)

- Thanh thép : \({\ell _{01}} = {\ell _{02}} + \Delta \ell  = 150 + 50 = 200mm\)