Giải bài 3.43 trang 90 SGK Toán 8 - Cùng khám phá
Cho
Đề bài
Cho \(ABCD\) là hình bình hành có góc \(C\) là góc nhọn. Trên tia đối của tia \(DC\) lấy điểm \(E\) sao cho \(AD = AE\) ( \(E\) khác \(D\)). Chứng minh rằng \(ABCE\) là một hình thang cân.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất hình bình hành và tính chất hình thang cân để chứng minh.
Lời giải chi tiết
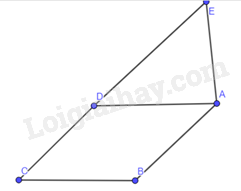
Ta có:
Tam giác \(ABCD\) là hình bình hành
→ \(AB//DC\)
Mà \(DE\) là cạnh đối của \(DC\)
→ \(AB//CE\)
→ Tứ giác \(ABCE\) là hình thang
Lại có: \(\widehat {DCB} = \widehat {EDA}\) (do hai góc này ở vị trí đồng vị)
Mà \(\widehat {EDA} = \widehat {DEA}\) (do tam giác \(AED\) cân)
→ \(\widehat {DCB} = \widehat {DEA}\)
→ Tứ giác \(ABCE\) là hình thang cân vì có hai góc kề 1 đáy bằng nhau.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3.43 trang 90 SGK Toán 8 - Cùng khám phá timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3.43 trang 90 SGK Toán 8 - Cùng khám phá timdapan.com"







