Bài 3.2 phần bài tập bổ sung trang 161 SBT toán 8 tập 1
Giải bài 3.2 phần bài tập bổ sung trang 161 sách bài tập toán 8. Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H...
Đề bài
Cho tam giác đều \(ABC\) và điểm \(M\) bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm \(M\) và vuông góc với \(BC\) tại điểm \(H.\) Đường thẳng đi qua điểm \(M\) và vuông góc với \(CA\) tại điểm \(K.\) Đường thẳng đi qua điểm \(M\) và vuông góc với \(AB\) tại điểm \(T.\)
Chứng minh rằng \(MH+MK+MT\) không phụ thuộc vào vị trí của điểm \(M.\)
Phương pháp giải - Xem chi tiết
Gợi ý: Tổng diện tích của tam giác \(MBC,\,MCA,\,MAB\) bằng tổng diện tích của tam giác \(ABC\)
Lời giải chi tiết
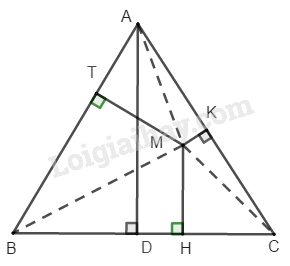
Giả sử \(∆ ABC\) đều có cạnh bằng \(a,\) kẻ đường cao \(AD,\) đặt \(AD = h\) không đổi.
Ta có:
\(\begin{array}{l}{S_{ABC}} = \dfrac{1}{2}ah\\{S_{MAB}} = \dfrac{1}{2}MT.a\\{S_{MAC}} = \dfrac{1}{2}MK.a\\{S_{MBC}} = \dfrac{1}{2}MH.a\\{S_{ABC}} = {S_{MAB}} + {S_{MAC}} + {S_{MBC}}\\\dfrac{1}{2}ah = \dfrac{1}{2}MT.a + \dfrac{1}{2}MK.a \\+ \dfrac{1}{2}MH.a\\\dfrac{1}{2}ah = \dfrac{1}{2}a(MT + MK + MH)\\ \Rightarrow MT + MK + MH = h\end{array}\)
\( \Rightarrow MT + MK + MH = h\) không đổi
Vậy tổng \(MT + MK + MH\) không phụ thuộc vào điểm \(M.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3.2 phần bài tập bổ sung trang 161 SBT toán 8 tập 1 timdapan.com"







