Bài 31 trang 134 Vở bài tập toán 8 tập 2

Đề bài

Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho ở hình 92c.

Lời giải chi tiết

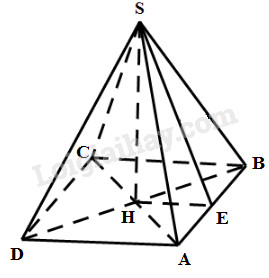
Theo giả thiết của bài toán đã cho ở trên, trong hình \(92c\). 

Ta có:

\(SA = SB = SC = SD = 10cm\)

\(AB = BC = CD = DA = 5cm\)

Gọi \(H\) là giao điểm hai đường chéo của đáy thì \(SH\) là chiều cao của hình chóp tứ giác đều đã cho. Ta có:

\(SHE\) là tam giác vuông tại \(H\), do đó \(SH = \sqrt {S{E^2} - H{E^2}} \).

Để tính được \(SH\) ta phải tính \(SE\) và \(HE\). 

\(SE = \sqrt {S{B^2} - B{E^2}} \) \( = \sqrt {{{10}^2} - {{\left( {\dfrac{5}{2}} \right)}^2}}  \approx 9,68\left( {cm} \right)\)

\(HE = \dfrac{{AB}}{2} = 2,5\left( {cm} \right)\)

\(SH =\sqrt {SE^2 - HE^2}\approx \sqrt {9,{{68}^2} - 2,{5^2}}  \approx 9,35\left( {cm} \right)\).