Giải Bài 3 trang 63 sách bài tập toán 7 tập 1 - Chân trời sáng tạo

Đề bài

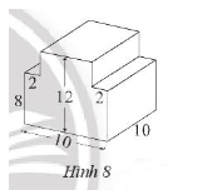
Một khối gỗ có kích thước như Hình 8 (đơn vị dm).

a) Tính thể tích của khối gỗ.

b) Tính diện tích toàn phần của khối gỗ.

Lời giải chi tiết

a) Quan sát Hình 8 ta thấy khối gỗ được ghép bởi hai khối hộp chữ nhật.

+ Khối hộp chữ nhật ở phía dưới có kích thước là 10 dm, 8 dm và 10 dm, do đó thể tích của khối hộp chữ nhật phía dưới là: V₁ = 10 . 8 . 10 = 800 (dm³).

+ Khối hộp chữ nhật ở phía trên có:

- Chiều dài là 10 dm;

- Chiều rộng là: 10 – 2 – 2 = 6 (dm);

- Chiều cao là: 12 – 8 = 4 (dm).

Thể tích của khối hộp chữ nhật ở phía trên là: V₂ = 10 . 6 . 4 = 240 (dm³).

Vậy thể tích của khối gỗ là V = V₁ + V₂ = 800 + 240 = 1 040 (dm³).

b) Có thể xem khối gỗ là hình lăng trụ có đáy hình gồm 2 hình chữ nhật ghép lại với nhau và chiều cao là h = 10 dm.

Chu vi đáy là: CV_đáy = 10 + 8 + 2 + 4 + 6 + 4 + 2 + 8 = 44 (dm).

Diện tích xung quanh của khối gỗ là: S_xq = CV_đáy . h = 44 . 10 = 440 (dm²).

Diện tích hai mặt đáy là: S_2đáy = 2 . (10 . 8 + 6 . 4) = 208 (dm²).

Diện tích toàn phần của khối gỗ là: S_tp = S_xq + S_2đáy = 440 + 208 = 648 (dm²).