Giải bài 3 trang 41 SGK Toán 10 tập 2 – Cánh diều
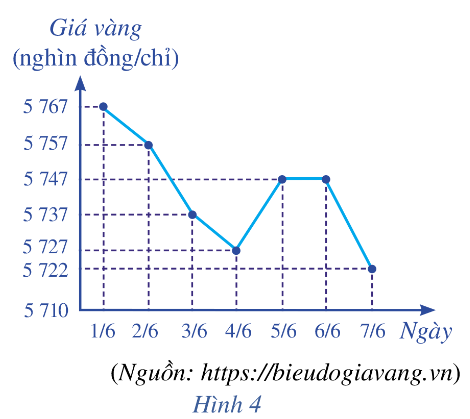
Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.
Đề bài
Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.
a) Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.
b) Tìm khoảng biến thiên của mẫu số liệu đó.
c) Tìm khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
Phương pháp giải - Xem chi tiết
a) Quan sát biểu đồ
b) Cho mẫu số liệu: \({x_1},{x_2},...,{x_n}\)
+) Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \({X_1},{X_2},...,{X_n}\)
+) Bước 2: Khoảng biến thiên: \(R = {X_n} - {X_1}\)
c) +) Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \({X_1},{X_2},...,{X_n}\)
+) Bước 2: \({Q_2} = {M_e} = \left\{ \begin{array}{l}{X_{k + 1}}\quad \quad \quad \quad \quad (n = 2k + 1)\\\frac{1}{2}({X_k} + {X_{k + 1}})\quad \;\,(n = 2k)\end{array} \right.\)
\({Q_1}\) là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
\({Q_3}\) là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\)
d) +) Tính phương sai \({s^2} = \frac{1}{n}\left[ {{{\left( {{x_1} - \overline x } \right)}^2} + {{\left( {{x_2} - \overline x } \right)}^2} + ... + {{\left( {{x_n} - \overline x } \right)}^2}} \right]\)
+) Độ lệch chuẩn \(s = \sqrt {{s^2}} \)
Lời giải chi tiết
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5767 5757 5747 5737 5727 5747 5747 5722
b) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 5767 - 5722 = 45\)
c) +) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5722 5727 5737 5747 5747 5747 5757 5767
+) Các tứ phân vị của mẫu số liệu là: \({Q_1} = 5732,{Q_2} = 5747,{Q_3} = 5762\)
+) Khoảng tứ phân vị của mẫu số liệu là: \({Q_3} - {Q_1} = 30\)
d) +) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là: \(\overline x = \frac{{5722{\rm{ + }}5727{\rm{ + }}5737{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5757{\rm{ + }}5767}}{8} = 5743,875\) ( nghìn đồng/ chỉ)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5722 - \overline x } \right)}^2} + {{\left( {5727 - \overline x } \right)}^2} + ... + {{\left( {5767 - \overline x } \right)}^2}} \right]}}{8} \approx 193,35\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} \approx 13,9\)( nghìn đồng/ chỉ)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3 trang 41 SGK Toán 10 tập 2 – Cánh diều timdapan.com"







