Giải bài 3 trang 122 sách bài tập toán 10 - Chân trời sáng tạo
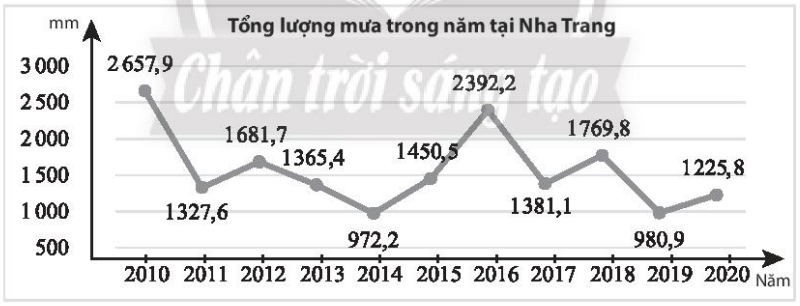
Tổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ 2010 đến 2020 được thể hiện trong biểu đồ sau ( đơn vị: mm).
Đề bài
Tổng lượng mưa trong năm tại một trạm quan trắc đặt tại Nha Trang từ 2010 đến 2020 được thể hiện trong biểu đồ sau (đơn vị: mm).
a) Hãy tính lượng mưa trung bình tại trạm quan trắc trên từ 2010 đến 2020.
b) Hãy tìm các tứ phân vị của mẫu số liệu đó.
Phương pháp giải - Xem chi tiết
- Dùng công thức tính số trung bình: \(\overline x = \frac{{{x_1} + {x_2} + ... + {x_n}}}{n}\)
- Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Lời giải chi tiết
a) Lượng mưa trung bình tại trạm quan trắc trên từ 2010 đến 2020 là:
\(\overline x = \frac{{2657,9 + 1327,6 + 1681,7 + 1365,4 + 972,2 + 1450,5 + 2392,2 + 1381,1 + 1769,8 + 980,9 + 1225,8}}{{11}} = 1564,1\)
b) Sắp xếp số liệu theo thứ tự không giảm ta được:
972,2 ;980,9; 1225,8; 1327,6; 1365,4; 1381,1; 1450,5; 1681,7; 1769,8; 2392,2; 2657,9.
Vì \(n = 11\)là số lẻ nên \({Q_2} = 1381,1\)
Tứ phân vị thứ nhất là trung vị của 5 số đầu \({Q_1} = 1225,8\)
Tứ phân vị thứ ba là trung vị của 5 số cuối \({Q_3} = 1769,8\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3 trang 122 sách bài tập toán 10 - Chân trời sáng tạo timdapan.com"