Bài 3. Cường độ trường hấp dẫn - Chuyên đề học tập Lí 11 Chân trời sáng tạo

KĐ

Các nhà khoa học đã tính toán được rằng, xét cùng một vật, khi lần lượt đặt trên bề mặt của Mặt Trăng và Trái Đất thì độ lớn lực hấp dẫn do Mặt Trăng tác dụng lên vật chỉ bằng khoảng 17% độ lớn lực hấp dẫn do Trái Đất tác dụng lên vật. Ta có thể khẳng định trường hấp dẫn của Mặt Trăng luôn yếu hơn Trái Đất hay không? Đại lượng nào đặc trưng cho độ mạnh yếu của trường hấp dẫn tại một điểm xác định trong không gian?

Lời giải chi tiết:

Do có khối lượng nhỏ hơn nhiều so với khối lượng của Trái Đất, nên Mặt trăng có trường hấp dẫn nhỏ hơn khoảng 1,6 lần tuy nhiên nếu không có lực hấp dẫn của nó, Trái Đất sẽ không có bầu khí quyển và mọi thứ cố định trên bề mặt Trái đất sẽ đơn giản là "trôi nổi" trong không gian trống rỗng.

Cường độ trường hấp dẫn là đại lượng đặc trưng cho độ mạnh yếu của trường hấp dẫn tại một điểm xác định trong không gian.

CH 1

Đặt vật có khối lượng m vào một vị trí xác định trong trường hấp dẫn do vật có khối lượng M sinh ra. Xác định tỉ số giữa độ lớn lực hấp dẫn do vật khối lượng M tác dụng lên vật khối lượng m. Tỉ số này có phụ thuộc vào giá trị m không?

Lời giải chi tiết:

Lực hấp dẫn do vật khối lượng M tác dụng lên vật khối lượng m là: \(F = G\frac{{Mm}}{{{r^2}}}\)

Tỉ số \(\frac{F}{m} = G\frac{M}{{{r^2}}} \Rightarrow \frac{F}{m}\)không phụ thuộc vào m mà chỉ phụ thuộc vào vị trí đặt vật trong trường hấp dẫn.

CH 2

Dựa vào công thức (3.1) và định luật vạn vật hấp dẫn, hãy rút ra các đặc điểm và biểu thức độ lớn của cường độ trường hấp dẫn.

Lời giải chi tiết:

Cường độ trường hấp dẫn cùng phương nối từ tâm vật tới điểm cần xét và có chiều hướng vào tâm của vật

độ lớn:\(g = G\frac{M}{{{r^2}}}\)

LT

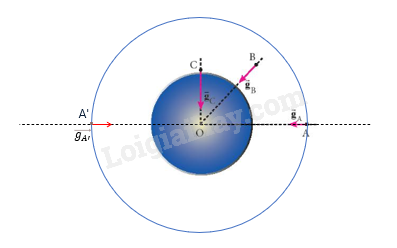
Trên Hình 3.2, hãy xác định ba điểm trên đường thẳng OA mà cường độ trường hấp dẫn có độ lớn nhỏ hơn, bằng và lớn hơn g_A. Biểu diễn vectơ cường độ trường hấp dẫn tại ba điểm đó.

Lời giải chi tiết:

Các điểm có r > OA và OA' thì có cường độ trường hấp dẫn nhỏ hơn g_A

Các điểm có r < OA và OA' thì có cường độ trường hấp dẫn lớn hơn g_A

tại A' thì g_A' = g_A

CH

Tính toán và nhận xét về độ lớn của cường độ trường hấp dẫn Trái Đất ở bề mặt và giá trị gia tốc trọng trường đã được học trong chương trình môn Vật lí ở lớp 10.

Lời giải chi tiết:

Cường độ trường hấp dẫn Trái Đất ở bề mặt: \[\frac{{G{M_{TD}}}}{{R_{TD}^2}} = \frac{{6,{{67.10}^{ - 11}}.5,{{97.10}^{24}}}}{{{{({{6373.10}^3})}^2}}} = 9,81m/{s^2}\]

Cường độ trường hấp dẫn Trái Đất ở bề mặt gần bằng gia tốc trọng trường

LT

Đỉnh Everest (Hình 3.3) là đỉnh núi cao nhất so với mực nước biển (bề mặt Trái Đất) và có độ cao là 8 849 m. Biết cường độ trường hấp dẫn tại bề mặt của Trái Đất (xét tại nơi có cùng vĩ độ) có độ lớn là 9,792 m/s². Xác định độ lớn cường độ trường hấp dẫn tại đỉnh Everest, nhận xét kết quả đạt được. Lấy bán kính Trái Đất tại đây khoảng 6 373 km.

Lời giải chi tiết:

Cường độ trường hấp dẫn tại đỉnh Everest là:

\(g = {g_0}{\left( {\frac{{{R_{TD}}}}{{{R_{TD}} + h}}} \right)^2} = 9,792.{\left( {\frac{{6373}}{{6373 + 8,849}}} \right)^2} = 9,765m/{s^2}\)

Cường độ trường hấp dẫn giảm nhưng không đáng kể. 

VD

Biết khối lượng và bán kính trung bình của Trái Đất lần lượt là 5,97.10²⁴ kg và 6 371 km. Trạm vũ trụ Quốc tế (ISS) ở độ cao 420 km so với bề mặt Trái Đất.

a) Xác định độ lớn của cường độ trường hấp dẫn do Trái Đất sinh ra tại vị trí của Trạm ISS.

b) Xác định độ lớn lực hấp dẫn của Trái Đất tác dụng lên một phi hành gia nặng 70 kg trên ISS.

c) Giải thích về hiện tượng “không trọng lượng" của các phi hành gia khi đang làm nhiệm vụ trên các tàu vũ trụ.

Lời giải chi tiết:

a) Cường độ trường hấp dẫn do Trái Đất sinh ra tại vị trí của Trạm ISS là:

\(g = {g_0}{\left( {\frac{{{R_{TD}}}}{{{R_{TD}} + h}}} \right)^2} = 9,792.{\left( {\frac{{6373}}{{6373 + 420}}} \right)^2} = 8,619m/{s^2}\)

b) Độ lớn lực hấp dẫn của Trái Đất tác dụng lên một phi hành gia nặng 70 kg trên ISS là:

F= g.m=8,619.70=603,301 (N)

c) Các phi hành gia cảm thấy "không trọng lượng" vì tàu con thoi của họ đang ở trạng thái rơi tự do liên tục xuống Trái Đất. Tuy nhiên, tàu con thoi không bao giờ rơi xuống Trái Đất vì nó đang di chuyển theo phương ngang với vận tốc khoảng 18.000 km / giờ, chống lại lực hấp dẫn. Nếu tàu vũ trụ không di chuyển đủ nhanh, nó sẽ rơi vào tình trạng ảnh hưởng của trường hấp dẫn của Trái Đất và rơi xuống Trái Đất.

Không có cái gọi là không trọng lực trong không gian. Lực hấp dẫn ở khắp mọi nơi trong vũ trụ và thể hiện ở các lỗ đen, quỹ đạo thiên thể, thủy triều và thậm chí cả trọng lượng của chính chúng ta.

LT

Biết bán kính và khối lượng trung bình của Trái Đất và Mặt Trăng lần lượt là R_TĐ = 6371 km, M_TĐ = 5,97.10²⁴ kg, R_MT=1737 km, M_MT= 7,35.10²²kg. Giải thích tại sao nhà du hành vũ trụ trên Mặt Trăng có thể dễ dàng nhảy lên cao (Hình 3.5) dù mang trên người bộ đồ rất nặng (khoảng 127 kg). (Nguồn: NASA)

Lời giải chi tiết:

Cường độ trường hấp dẫn tại Trái Đất là:

\[{g_{TD}} = \frac{{G{M_{TD}}}}{{R_{TD}^2}} = \frac{{6,{{67.10}^{ - 11}}.5,{{97.10}^{24}}}}{{{{({{6371.10}^3})}^2}}} = 9,81m/{s^2}\]

Cường độ trường hấp dẫn tại Mặt Trăng là:

\[{g_{MT}} = \frac{{G{M_{MT}}}}{{R_{MT}^2}} = \frac{{6,{{67.10}^{ - 11}}.7,{{35.10}^{22}}}}{{{{({{1737.10}^3})}^2}}} = 1,63m/{s^2}\]

Vì cường độ trường hấp dẫn tại Trái Đất lớn hơn so với tại Mặt Trăng nên trọng lực của nhà du hành vũ trụ tại Mặt Trăng nhỏ hơn nên trên Mặt Trăng có thể dễ dàng nhảy lên cao.

VD

So sánh độ lớn cường độ trường hấp dẫn trên bề mặt của Hỏa Tinh và Trái Đất.

Lời giải chi tiết:

Cường độ trường hấp dẫn trên bề mặt của Hỏa Tinh là:

\[{g_{HT}} = \frac{{G{M_{HT}}}}{{R_{HT}^2}} = \frac{{6,{{67.10}^{ - 11}}.6,{{42.10}^{23}}}}{{{{({{3300.10}^3})}^2}}} = 3,73m/{s^2}\]

Cường độ trường hấp dẫn trên bề mặt của Trái Đất là:

\[{g_{TD}} = \frac{{G{M_{TD}}}}{{R_{TD}^2}} = \frac{{6,{{67.10}^{ - 11}}.5,{{97.10}^{24}}}}{{{{({{6373.10}^3})}^2}}} = 9,81m/{s^2}\]

Cường độ trường hấp dẫn trên bề mặt Hỏa Tinh nhỏ hơn so vơi Trái Đất.

Bài 1

Cường độ trường hấp dẫn tại bề mặt trên đường xích đạo của Mộc Tinh có độ lớn 25 m/s². Xác định khối lượng của Mộc Tinh, biết bán kính xích đạo của hành tinh này khoảng 7,14.10⁷ m.

Lời giải chi tiết:

Ta có: \(g = \frac{{GM}}{{{R^2}}} \Rightarrow M = \frac{{g{R^2}}}{G} = \frac{{25.7,{{14.10}^7}}}{{6,{{67.10}^{ - 11}}}} = 2,{672.10^{19}}kg\)

Vậy khối lượng của Mộc Tinh là: 2,672.10¹⁹kg

Bài 2

Hoả Tinh là hành tinh gần Trái Đất nhất nếu tính khoảng cách từ Mặt Trời, có khối lượng 6,42.10²³kg, và bán kính 3 390 km.

a. Xác định độ lớn trường hấp dẫn trên bề mặt Hoả Tinh.

b. Xác định trọng lượng của một người nặng 60 kg đứng trên bề mặt Hỏa Tinh.

c. So sánh với trọng lượng của người này khi đứng trên bề mặt Trái Đất.

Lời giải chi tiết:

a. Cường độ trường hấp dẫn trên bề mặt của Hỏa Tinh là:

\[{g_{HT}} = \frac{{G{M_{HT}}}}{{R_{HT}^2}} = \frac{{6,{{67.10}^{ - 11}}.6,{{42.10}^{23}}}}{{{{({{3300.10}^3})}^2}}} = 3,73m/{s^2}\]

b. Trọng lượng của một người nặng 60 kg đứng trên bề mặt Hỏa Tinh là: P=m.g_HT=70.3,73=261,1(N)

c. Trọng lượng của người này khi đứng trên bề mặt Trái Đất là: P=m.g_TD=70.9,81=686,7 (N)

Trọng lượng của người này trên Hỏa Tinh nhẹ hơn khi ở trên Trái Đất.