Bài 29 trang 134 Vở bài tập toán 9 tập 1

Đề bài

Cho hai đường tròn \((O;\ 20cm)\) và \((O'; 15cm)\) cắt nhau tại \(A\) và \(B\). Tính đoạn nối tâm \(OO'\), biết rằng \(AB=24cm.\) (Xét hai trường hợp: \(O\) và \(O'\) nằm khác phía đối với \(AB;\ O\) và \(O'\) nằm cùng phía đối với \(AB\)).

Lời giải chi tiết

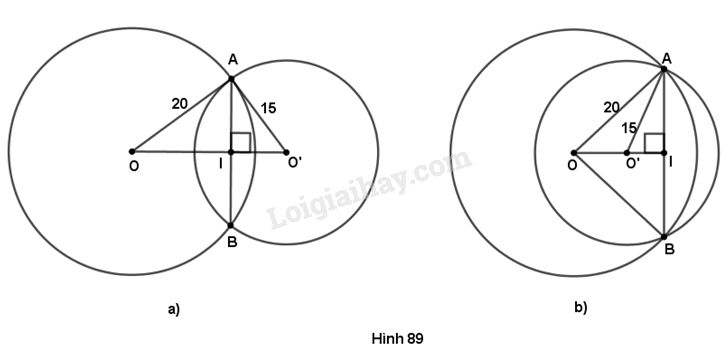
Gọi \(I\) là giao điểm của \(OO'\) và \(AB.\) Theo tính chất hai đường tròn cắt nhau, ta có \(OO'\) là đường trung trực của \(AB,\) do đó

\(OO'\bot AB\) và \(AI=IB=\dfrac{AB}{2}\)\(=\dfrac{24}{2}=12\left( cm \right).\)

Tính \(OI:\) Áp dụng định lí Py-ta-go cho tam giác vuông \(AIO,\) ta có

\(O{{I}^{2}}=O{{A}^{2}}-A{{I}^{2}}\)\(={{20}^{2}}-{{12}^{2}}=400-144=256.\)

Suy ra \(OI = 16cm.\)

Tính \(O'I:\) Áp dụng định lí Py-ta-go cho tam giác vuông \(AIO',\) ta có

\(O'{{I}^{2}}=O'{{A}^{2}}-A{{I}^{2}}={{15}^{2}}-{{12}^{2}}\)\(=225-144=81\left( cm \right).\)

Suy ra \(O'I=9cm.\)

Xét hai trường hợp :

a) Nếu \(O\) và \(O'\) nằm khác phía đối với \(AB\) thì

\(OO' = OI + IO' = 16 + 9 = 25\left( {cm} \right).\)

b) Nếu \(O\) và \(O'\) nằm cùng phía đối với \(AB\) thì

\(OO' = OI - IO' = 16 - 9 = 7\left( {cm} \right).\)