Bài 28 trang 91 Vở bài tập toán 8 tập 2
Giải bài 28 trang 91 VBT toán 8 tập 2. Tính độ dài x của đoạn thẳng BD trong hình ...
Đề bài
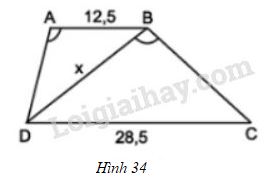
Tính độ dài \(x\) của đoạn thẳng \(BD\) trong hình 34 (Làm tròn đến chữ thập phân thứ nhất), biết rằng \(ABCD\) là hình thang (\(AB // CD\)); \(AB= 12,5cm; CD= 28,5cm\); \(\widehat{DAB} = \widehat{DBC}\).
Phương pháp giải - Xem chi tiết
Áp dụng:
- Định lí: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Tính chất hai tam giác đồng dạng, tia phân giác.
Lời giải chi tiết
Xét \(ABD\) và \(BDC\)
Ta có: \(\widehat{DAB}\) = \(\widehat{DBC}\) (theo giả thiết)
\(\widehat{ABD}\) = \(\widehat{BDC}\) (hai góc so le trong)
Do đó \( ∆ABD ∽ ∆BDC\) (Trường hợp đồng dạng thứ ba).
Suy ra \(\dfrac{AB}{BD} = \dfrac{BD}{DC}\) \( \Leftrightarrow B{D^2} = AB.DC\)
hay \(x^2=12,5.28,5\) \( \Leftrightarrow x = \sqrt {12,5.28,5} \)
Tính trên máy tính bỏ túi (và làm tròn số) được \( x \approx 18,9 cm\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 28 trang 91 Vở bài tập toán 8 tập 2 timdapan.com"







