Bài 27 trang 90 Vở bài tập toán 8 tập 2

Đề bài

Chứng minh rằng nếu tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) theo tỉ số \(k\) thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng \(k\).

Lời giải chi tiết

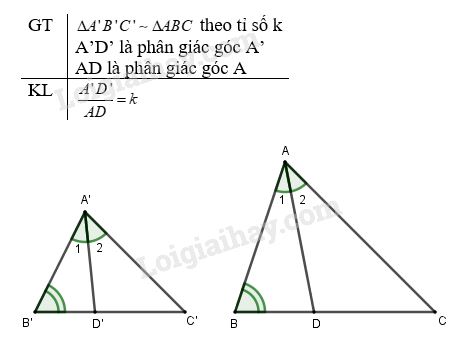
Chứng minh:

Từ giả thiết \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số \(k\), suy ra

\(\widehat {A'} = \widehat A;\widehat {B'} = \widehat B;\widehat {C'} = \widehat C;\) \(\dfrac{{A'B'}}{{AB}} = \dfrac{{A'C'}}{{AC}} = \dfrac{{B'C'}}{{BC}} = k\).

Xét hai tam giác \(A'B'D'\) và \(ABD\):

\(\widehat {{A_1}'} = \dfrac{1}{2}\widehat {A'};\widehat {{A_1}} = \dfrac{1}{2}\widehat A;\) mà \(\widehat {A'} = \widehat A\) (theo kết quả trên).

Do đó \(\widehat {{A_1}'} = \widehat {{A_1}}\) (1)

Ta lại có: \(\widehat {B'} = \widehat B\) (2) (theo kết quả trên).

Từ định lí (của trường hợp đồng dạng thứ ba) suy ra \(\Delta A'B'D' \backsim \Delta ABD\)

Suy ra \(\dfrac{{A'D'}}{{AD}} = \dfrac{{A'B'}}{{AB}} = k\) (đpcm).