Bài 28 trang 49 Vở bài tập toán 7 tập 2

Đề bài

Trong các số cho ở bên phải mỗi đa thức, số nào là bậc của đa thức đó ?

Lời giải chi tiết

Bậc của đa thức là số được khoanh tròn trong bảng sau :

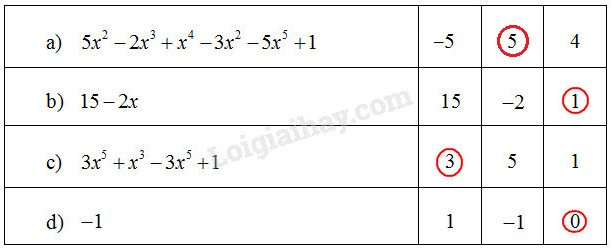
Giải thích:

a) Rút gọn

\(\eqalign{
& 5{x^2}-2{x^3} + {x^4}-3{x^2}-5{x^5} + 1 \cr 
& = \left( {5{x^2} - 3{x^2}} \right) - 2{x^3} + {x^4} - 5{x^5} + 1 \cr 
& = 2{x^2} - 2{x^3} + {x^4} - 5{x^5} + 1 \cr} \)

Bậc của đa thức \(2{x^2} - 2{x^3} + {x^4} - 5{x^5} + 1\) là \(5\). 

b) Bậc của đa thức \(15 - 2x\) là \(1\).

c) Ta có:

\(\eqalign{
& 3{x^5} + {x^3}-3{x^5} + 1 \cr 
& = \left( {3{x^5} - 3{x^5}} \right) + {x^3} + 1 \cr 
& = {x^3} + 1 \cr} \)

Bậc của đa thức \(3{x^5} + {x^3}-3{x^5} + 1\) là bậc của đa thức \( {x^3} + 1\) là \(3\).

d) Bậc của đa thức \(-1\)  là \(0\) (Mọi số thực khác \(0\) là đơn thức bậc không).