Bài 27 trang 100 Vở bài tập toán 7 tập 1
Giải bài 27 trang 100 VBT toán 7 tập 1. Tại sao lại sử dụng tiên đề Ơclit thì suy ra được tính chất: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau?
Đề bài
Tại sao lại sử dụng tiên đề Ơclit thì suy ra được tính chất: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau?
Phương pháp giải - Xem chi tiết
Tiên đề Ơclit: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Lời giải chi tiết
Xem hình \(22\).
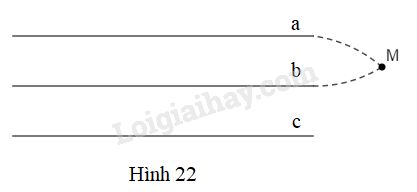
Biết \(a//c\) và \(b//c\) ta phải suy ra \(a//b\).
Ta suy luận như sau:
Giả sử hai đường thẳng phân biệt \(a\) và \(b\) không song song với nhau thì chúng phải cắt nhau tại \(M\). Khi đi qua \(M\) có hai đường thẳng \(a,\,b\) cùng song song với đường thẳng \(c\), điều đó trái với tiên đề Ơclit. Vậy điều giả sử trên là sai, ta có \(a//b\).
Cách suy luận khác. Xem hình \(23\).
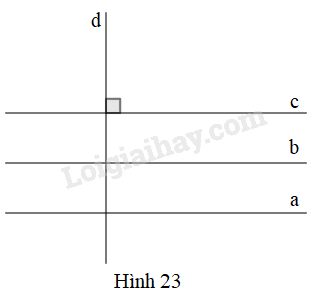
Vẽ \(d\bot c.\)
Vì \(a//c\) nên \(d\bot a\) (1)
Vì \(b//c\) nên \(d\bot b\) (2)
Từ (1) và (2), do \(a\) và \(b\) cùng vuông góc với \(d\) nên \(a//b\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 27 trang 100 Vở bài tập toán 7 tập 1 timdapan.com"







