Bài 2.48 trang 83 SBT hình học 11
Giải bài 2.48 trang 83 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy là tứ giác ABCD. Gọi G1 và G1 lần lượt là trọng tâm của các tam giác SBC và SCD...
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là tứ giác \(ABCD\). Gọi \(G_1\) và \(G_2\) lần lượt là trọng tâm của các tam giác \(SBC\) và \(SCD\)
Tìm giao tuyến của mặt phẳng \((AG_1G_2)\) với các mặt phẳng \((ABCD)\) và \((SCD)\).
Xác định thiết diện của hình chóp với mặt phẳng \((AG_1G_2)\).
Phương pháp giải - Xem chi tiết
- Sử dụng tính chất: "Nếu mặt phẳng \((\alpha )\) song song với đường thẳng \(a\) nằm trong mặt phẳng \((\beta )\) thì \((\alpha )\) cắt \((\beta )\) theo giao tuyến \(b//a\)".
- Tìm các giao tuyến của \((AG_1G_2)\) với các mặt của hình chóp suy ra thiết diện.
Lời giải chi tiết
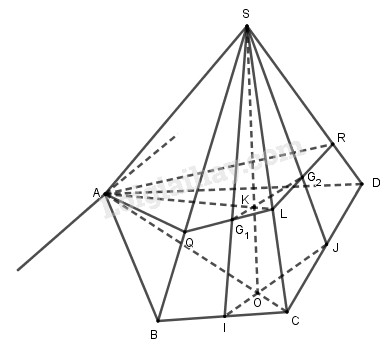
Gọi \(I, J\) lần lượt là trung điểm của \(BC, CD\).
Ta có \(IJ\parallel {G_1}{G_2}\) nên giao tuyến của hai mặt phẳng \((AG_1G_2)\) và \((ABCD)\) là đường thẳng \(d\) qua \(A\) và song song với \(IJ\)
Gọi \(O = IJ \cap AC,\) \(K = {G_1}{G_2} \cap SO,L = AK \cap SC\)
\(LG_2\) cắt \(SD\) tại \(R\)
\(LG_2\) cắt \(SB\) tại \(Q\)
Khi đó \(\left( {A{G_1}{G_2}} \right) \cap \left( {SCD} \right) = LR\)
Ta có thiết diện là tứ giác \(AQLR\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.48 trang 83 SBT hình học 11 timdapan.com"







