Bài 2.46 trang 83 SBT hình học 11
Giải bài 2.46 trang 83 sách bài tập hình học 11. Cho hình chóp S.ABCD, có đáy là hình bình hành. Gọi C’ là trung điểm của SC và M là một điểm di động trên cạnh SA. Mặt phẳng (P) di động luôn đi qua C’M và song song với BC...
Đề bài
Cho hình chóp S.ABCD, có đáy là hình bình hành. Gọi C’ là trung điểm của SC và M là một điểm di động trên cạnh SA. Mặt phẳng (P) di động luôn đi qua C’M và song song với BC.
a) Xác định thiết diện (P) cắt hình chóp S.ABCD. Xác định vị trí điểm M để thiết diện là hình bình hành.
b) Khi M di động trên cạnh SA, thì giao điểm của hai cạnh đối của thiết diện chạy trên đường nào?
Phương pháp giải - Xem chi tiết
Sử dụng tính chất: "Nếu mặt phẳng \((\alpha )\) song song với đường thẳng \(a\) nằm trong mặt phẳng \((\beta )\) thì \((\alpha )\) cắt \((\beta )\) theo giao tuyến \(b//a\)".
Lời giải chi tiết
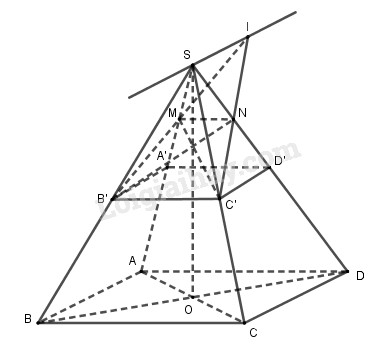
a) \(\left( P \right)\parallel BC\) nên (P) sẽ cắt (SBC) theo giao tuyến B’C’ song song với BC.
Tương tự, (P) cắt (SAD) theo giao tuyến MN song song với AD.
Khi M trùng với trung điểm A’ của cạnh SA thì thiết diện MB’C’N’ là hình bình hành.
b) Với M không trùng với A’:
Gọi \(I \in B'M \cap C'N\). Ta có:
\(I \in B'M \subset \left( {SAB} \right)\), tương tự \(I' \in C'N \subset \left( {SC{\rm{D}}} \right)\)
Như vậy \(I \in \Delta = \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.46 trang 83 SBT hình học 11 timdapan.com"







