Bài 20 trang 106 Vở bài tập toán 6 tập 2
Giải bài 20 trang 106 VBT toán 6 tập 2. Hình 20 cho biết hai tia AM và AN đối nhau, góc MAP bằng 33 độ, góc NAQ bằng 58 độ, tia AQ nằm giữa hai tia AN và AP. Tính số đo x của góc PAQ...
Đề bài
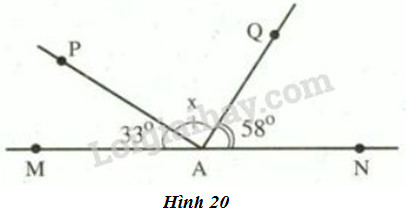
Hình 20 cho biết hai tia \(AM\) và \(AN\) đối nhau,\(\widehat{MAP}= 33^{0} , \widehat{NAQ}= 58^{0},\) tia \(AQ\) nằm giữa hai tia \(AN\) và \(AP ,\) Hãy tính số đo \(x\) của \(\widehat{PAQ}\)
Phương pháp giải - Xem chi tiết
Nếu \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\).
Hai góc kề bù thì có tổng số đo bằng \(180\) độ.
Tính \(\widehat {PAN}\) (góc kề bù với \(\widehat {MAP}\))
• Tính \(x\) từ hệ thức : \(\widehat {NAQ}+x=\widehat {PAN}\)
Lời giải chi tiết
Vì \(AM\) và \(AN\) là hai tia đối nhau nên \(\widehat{MAN}=180^\circ\)
\(\widehat{MAN}=\widehat{MAP}+\widehat{PAN}\)
Suy ra \(\widehat{PAN}={180^\circ} - {33^\circ} = {147^\circ}\)
Vì tia \(AQ\) nằm giữa hai tia \(AN\) và \(AP\)
Suy ra \(\widehat{PAN}=\widehat{PAQ}+\widehat{QAN}\)
Hay \(147^\circ= x + 58^\circ \)
Nên \(x = 147^\circ-58^\circ=89^\circ\)
Vậy \(\widehat{PAQ}=89^\circ\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 20 trang 106 Vở bài tập toán 6 tập 2 timdapan.com"







