Giải bài 2 trang 111 SGK Toán 8 tập 1 - Cánh diều

Đề bài

Cho tam giác ABC vuông tại A có M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh tứ giác ABCD là hình chữ nhật và \(AM = \dfrac{1}{2}BC\).

Lời giải chi tiết

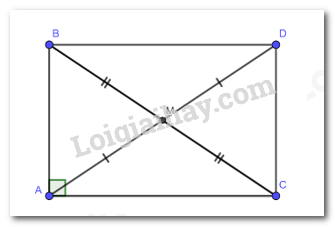
Xét tứ giác ABCD có:

MB = MC (M là trung điểm của BC)

MA = MD (gt)

Suy ra tứ giác ABPC là hình bình hành (có hai đường chéo cắt nhau tại trung điểm của mỗi đường)

Mà hình bình hành ABDC có \(\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over A}  = {90^0}\)nên ABCD là hình chữ nhật

Vì: ABDC là hình chữ nhật nên BC = AD

Mà: \(AM = \dfrac{1}{2}AC = \dfrac{1}{2}BC\)