Bài 18 trang 125 Vở bài tập toán 8 tập 2

Đề bài

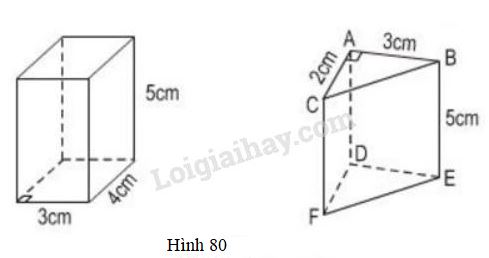
Tính diện tích xung quanh, diện tích toàn phần của các lăng trụ đứng sau đây :

Lời giải chi tiết

Tính diện tích xung quanh và diện tích toàn phần của hình lăng trụ đứng tứ giác:

\(\begin{array}{l}
{S_{xq}} = 2.p.h = 2\left( {3 + 4} \right).5 = 70\left( {c{m^2}} \right)\\
{S_{tp}} = {S_{xq}} + 2{S_{day}} = 70 + 2.3.4 = 94\left( {c{m^2}} \right)
\end{array}\)

Tính diện tích xung quanh và diện tích toàn phần của hình lăng trụ đứng tam giác \(ABC.DEF\):

Xét tam giác vuông \(ABC\) ta có:

\(BC = \sqrt {A{B^2} + A{C^2}} \) \( = \sqrt {{3^2} + {2^2}}  = \sqrt {13}  \approx 3,6\left( {cm} \right).\)

\({S_{xq}} = 2.p.h = \left( {2 + 3 + \sqrt {13} } \right).5\) \( = \left( {5 + \sqrt {13} } \right).5 \approx 43\left( {c{m^2}} \right)\)

\({S_{tp}} = {S_{xq}} + 2{S_{day}}\) \( \approx 43 + 2.\dfrac{1}{2}.2.3 = 49\left( {c{m^2}} \right)\)