Bài 17.4, 17.5, 17.6 trang 42 SBT Vật lí 10
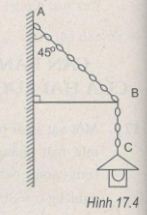
Giải bài 17.4, 17.5, 17.6 trang 42 sách bài tập vật lý 10. Một chiếc đèn có trọng lượng P = 40 N được treo vào tường nhờ một dây xích. Muốn cho đèn ở xa tường người ta dùng một thanh chống nằm ngang, một đầu tì vào tường còn đầu kia tì vào điểm B của dây xích (H.17.4). Bỏ qua trọng lượng của thanh chống, dây xích và ma sát ở chỗ thanh tiếp xúc với tường. Cho biết dây xích hợp với tường một góc 45°.
17.4.
Một chiếc đèn có trọng lượng P = 40 N được treo vào tường nhờ một dây xích. Muốn cho đèn ở xa tường người ta dùng một thanh chống nằm ngang, một đầu tì vào tường còn đầu kia tì vào điểm B của dây xích (H.17.4). Bỏ qua trọng lượng của thanh chống, dây xích và ma sát ở chỗ thanh tiếp xúc với tường. Cho biết dây xích hợp với tường một góc 45°.
a) Tính lực căng của các đoạn xích BC và AB.
b) Tính phản lực Q của tường lên thanh.
Phương pháp giải:
Sử dụng lí thuyết về điều kiện cân bằng của vật rắn: muốn cho một chất điểm đứng cân bằng thì hợp lực của các lực tác dụng lên nó phải bằng 0
Lời giải chi tiết:
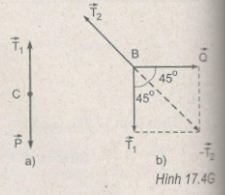
Điểm C đứng cân bầng (H.17.4Ga), nên:
T1= P = 40 N
Thanh chống đứng cân bằng (H. 17.4Gb),
ba lực \(\overrightarrow {{T_1}} ,\overrightarrow {{T_2}} \) và \(\overrightarrow {{Q}}\) đồng quy ở B. Từ tam giác lực, ta có :
Q = T1 = P = 40 N
T2= T1 \(\sqrt 2 \) = 56,4 ≈ 56 N.
Chú ý: Do tường không có ma sát nên xích phải có ma sát mới giữ được thanh chống, vì vậy T2 phải lớn hơn T1.
17.5.
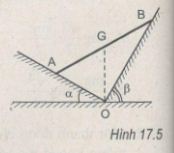
Một thanh AB đồng chất, khối lượng m = 2,0 kg tựa lên hai mặt phẳng nghiêng không ma sát, với các góc nghiêng α = 30° và β = 60°. Biết giá của trọng lực của thanh đi qua giao tuyến O của hai mặt phẳng nghiêng (H.17.5). Lấy g = 10 m/s2. Xác định áp lực của thanh lên mỗi mặt phẳng nghiêng.
Phương pháp giải:
- Sử dụng lí thuyết về phân tích lực, vẽ các lực tác dụng lên vật
- Sử dụng các hệ thức lượng giác sin, cos trong tam giác vuông
Lời giải chi tiết:
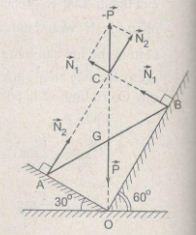
Thanh AB chịu ba lực cân bàng là \(\overrightarrow P ,\overrightarrow {{N_1}} \) và \(\overrightarrow {{N_2}} \) . Vì mặt phẳng nghiêng không ma sát nên hai phản lực \(\overrightarrow {{N_1}} \) và \(\overrightarrow {{N_2}} \)vuông góc với các mặt phẳng nghiêng. Ta trượt các vectơ lực trên giá của chúng đến điểm đồng quy C (H.17.5G).
Từ tam giác lực, ta được:
N1 = Psin30° = 20.0,5 = 10 N
N2= Pcos30° = 20.\(\displaystyle{{\sqrt 3 } \over 2}\) = 17,3 ≈ 17 N
Theo định luật III Niu-tơn thì áp lực của thanh lên mặt phẳng nghiêng có độ lớn bằng phản lực của mặt phẳng nghiêng lên thanh.
17.6.
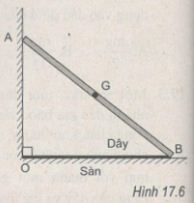
Một thanh gỗ đồng chất, khối lượng m = 3 kg được đặt dựa vào tường. Do tường và sàn đều không có ma sát nên người ta phải dùng một dây buộc đầu dưới B của thanh vào chân tường để giữ cho thanh đứng yên (H.17.6). Cho biết OA = OB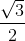 
và lấy g = 10 m/s2. Xác định lực căng T của dây.
Phương pháp giải:
- Sử dụng lí thuyết về phân tích lực, vẽ các lực tác dụng lên vật
- Sử dụng các hệ thức lượng giác tan trong tam giác vuông
Lời giải chi tiết:
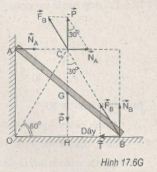
Gọi \(\overrightarrow {{F_B}} \) là hợp lực của lực căng \(\overrightarrow {{T}} \) và phản lực \(\overrightarrow {{N_B}} \) của sàn. Ta có hệ ba lực cân bằng là \(\overrightarrow P ,\overrightarrow {{N_A}} \) và \(\overrightarrow {{N_B}}\) . Ba lực này đồng quy tại C (H.17.6G).
Vì OA = CH = OB \(\displaystyle{{\sqrt 3 } \over 2}\) nên tam giác OCB là tam giác đều. Từ tam giác lực ta có :
T = NA= P.tan30° = \(\displaystyle{P \over {\sqrt 3 }}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 17.4, 17.5, 17.6 trang 42 SBT Vật lí 10 timdapan.com"
